Question

【题目】问题探究

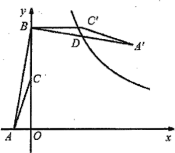
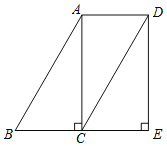
（1）请在图①的的边上求作一点，使最短；

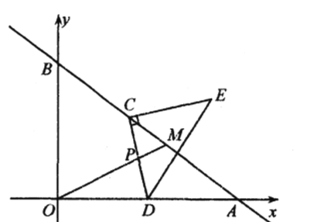
（2）如图②，点为内部一点，且满足．求证：点到点、、的距离之和最短，即最短；

问题解决

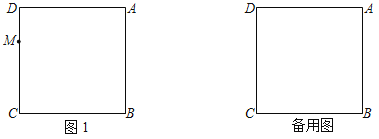
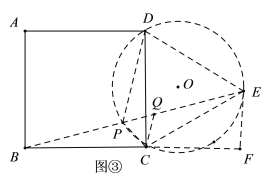
（3）如图③，某高校有一块边长为400米的正方形草坪，现准备在草坪内放置一对石凳及垃圾箱在点处，使点到、、三点的距离之和最小，那么是否存在符合条件的点？若存在，请作出点的位置，并求出这个最短距离；若不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）证明见解析；（3）存在，作图见解析；点到三点的距离之和最小值为米．

【解析】

（1）根据垂线段最短、利用尺规作图作出点P；

（2）将绕点逆时针旋转，得到，将绕点逆时针旋转，得到，连接，，，根据作图可知和均为等边三角形，连接，根据两点之间线段最短可知，当时，短，

（3）以BC为边作正△BCD，使点D与点A在BC两侧，作△BCD的外接圆，连接AD交圆于P，连接PB，作DE⊥AC交AC的延长线于E，根据勾股定理、直角三角形的性质计算，得到答案．

解：（1）如图①，过点作的垂线，

垂足为，点记为所求；

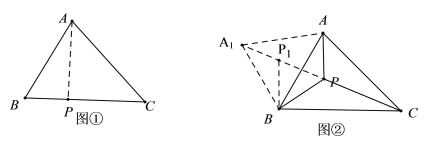
（2）如图②，将绕点逆时针旋转，得到，

将绕点逆时针旋转，得到，

连接，，，

根据作图可知和均为等边三角形，

∴，，

，

∴，

∴，

∴，

∴，

∴，

连接，根据两点之间线段最短可知，

当时，

最短，

∵，

∴，

又∵为等边三角形，

∴四点共线，

∴，

∴当时，最短；

（3）存在符合条件的点．

如解图③，以为作等边，在作的外接圆，

连接，交于点，

此时最小，

在上截取．

∵在等边中，

∴（同弧所对的圆周角相等）

∴为等边三角形，

∴．

∴．

∴．

又∵，，

∴，

∴，

∴最小．

理由如下：

设点为正方形内任意一点，

连接，、，

将绕点顺时针旋转得到．

∵，

∴为的最短距离．

在中，，米，

∴（米），

（米），

∴（米）．

在中，

．

∴点到三点的距离之和最小值为米．