题目内容
 已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F.(1)求证:AM=DM;
(2)若DF=2,求菱形ABCD的周长.
分析:(1)易证△AME是等腰三角形.则AM=AE=
AB=
AD,就可以证出;
(2)同理可以证出△DFM是等腰三角形,则DF=
AD,就可以求出边长,求出周长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)同理可以证出△DFM是等腰三角形,则DF=
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是菱形,
∴∠BAC=∠DAC.
又∵EF⊥AC,
∴AC是EM的垂直平分线,
∴AE=AM,
∵AE=AM=
AB=
AD,
∴AM=DM.
(2)解:∵AB∥CD,
∴∠AEM=∠F.
又∵∠FMD=∠AME,∠AME=∠AEM,
∴∠FMD=∠F,
∴△DFM是等腰三角形,
∴DF=DM=
AD.
∴AD=4.
∴菱形ABCD的周长是16.
∴∠BAC=∠DAC.

又∵EF⊥AC,
∴AC是EM的垂直平分线,
∴AE=AM,
∵AE=AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴AM=DM.
(2)解:∵AB∥CD,
∴∠AEM=∠F.
又∵∠FMD=∠AME,∠AME=∠AEM,
∴∠FMD=∠F,
∴△DFM是等腰三角形,
∴DF=DM=
| 1 |
| 2 |
∴AD=4.
∴菱形ABCD的周长是16.
点评:本题主要考查了等腰三角形的性质,等边对等角.线段的垂直平分线的性质,线段垂直平分线上的点,到线段两端的距离相等.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
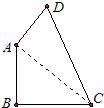 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.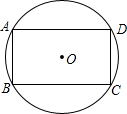 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.