题目内容
正方形ABCD的边长为1,以A为圆心,1为半径做⊙A,则点B在⊙A________,C点在⊙A________,D点在⊙A________.
上 外 上
分析:根据正方形的性质,可以求出AB,AC,AD的长,把它们的长与半径比较,可以确定B,C,D的位置.
解答:∵正方形的边长相等,∴AB=AD=1,又⊙A的半径是1,∴点B和点D在⊙A上.
用勾股定理可以求出正方形的对角线AC= >1,∴点C在圆外.
>1,∴点C在圆外.
故答案分别是:上,外,上.
点评:本题考查的是点与圆的位置关系,运用正方形的性质可以求出AB,AC,AD的长,然后与圆的半径作比较,确定点B,C,D与⊙A的位置关系.
分析:根据正方形的性质,可以求出AB,AC,AD的长,把它们的长与半径比较,可以确定B,C,D的位置.
解答:∵正方形的边长相等,∴AB=AD=1,又⊙A的半径是1,∴点B和点D在⊙A上.
用勾股定理可以求出正方形的对角线AC=
 >1,∴点C在圆外.
>1,∴点C在圆外.故答案分别是:上,外,上.
点评:本题考查的是点与圆的位置关系,运用正方形的性质可以求出AB,AC,AD的长,然后与圆的半径作比较,确定点B,C,D与⊙A的位置关系.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 附加题
附加题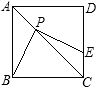 如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3
如图,正方形ABCD的边长为4,P为对角线AC上一点,且CP=3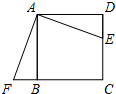 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为 如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=
如图,正方形ABCD的边长为6,点M在边DC上,M,N两点关于对角线AC对称,若DM=2,则tan∠ADN=