Question

【题目】【题目】如图，在平面直角坐标系中，一次函数y＝ax＋b(a≠0)的图象与反比例函数y＝ (k≠0)的图象交于第二、四象限内的A、B两点，与y轴交于C点，过点A作AH⊥y轴，垂足为H，OH＝3，tan∠AOH＝，点B的坐标为(m，－2)．

(1)求△AHO的周长；

(2)求该反比例函数和一次函数的解析式．

Answer 1

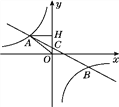
【答案】(1)△AHO的周长为12；(2) 反比例函数的解析式为y＝，一次函数的解析式为y＝－x＋1.

【解析】试题分析: （1）根据正切函数，可得AH的长，根据勾股定理，可得AO的长，根据三角形的周长，可得答案；

（2）根据待定系数法，可得函数解析式．

试题解析：（1）由OH=3，tan∠AOH=，得

AH=4．即A（-4，3）．

由勾股定理，得

AO==5，

△AHO的周长=AO+AH+OH=3+4+5=12；

（2）将A点坐标代入y=（k≠0），得

k=-4×3=-12，

反比例函数的解析式为y=；

当y=-2时，-2=，解得x=6，即B（6，-2）．

将A、B点坐标代入y=ax+b，得

，

解得，

一次函数的解析式为y=-x+1．