题目内容
请回答: 能否表示为3个互异的正整数的倒数的和?
能否表示为3个互异的正整数的倒数的和? 能否表示为3个互异的完全平方数的倒数的和?如果能,请给出一个例子;如果不能,请说明理由.
能否表示为3个互异的完全平方数的倒数的和?如果能,请给出一个例子;如果不能,请说明理由.
解:(1)由于 ,
,
故有 .
.
所以, 能表示为3个互异的正整数的倒数的和(表示法不唯一).
能表示为3个互异的正整数的倒数的和(表示法不唯一).
(2)不妨设a<b<c,
现在的问题就是寻找整数a,b,c,
满足
由a<b<c,则有,
从而 ,
,
所以a2<24.又有 ,
,
所以a2>8,故a2=9或16.
若a2=9,则有 ,
,
由于 ,并且
,并且 ,
,
所以b2>72,72<b2<144.
故b2=81,100或121.将b2=81、100和121分别代入 ,没有一个是完全平方数,
,没有一个是完全平方数,
说明当a2=9时, 无解.
无解.
若a2=16,则 .
.
类似地,可得:16<b2<32,即b2=25,
此时, 不是整数.
不是整数.
综上所述, 不能表示为3个互异的完全平方数的倒数之和.
不能表示为3个互异的完全平方数的倒数之和.
评分参考:①正确回答第一问给(答案不唯一);
②能得到a2=9或16,给;
③能分别对a2=9和16讨论 能否表示为3个互异的完全平方数的倒数之和,各给,共;
能否表示为3个互异的完全平方数的倒数之和,各给,共;
④对代数式合理和正确的推导适当给分.
特别说明:因为各题的解答未必唯一,上述解答和评分仅供参考.
分析:(1)由 证明即可;
证明即可;
(2)设a<b<c,寻找满足 的整数.
的整数.
点评:此题利用分式的混合运算证明,难度较大,需要反复尝试.
 ,
,故有
 .
.所以,
 能表示为3个互异的正整数的倒数的和(表示法不唯一).
能表示为3个互异的正整数的倒数的和(表示法不唯一).(2)不妨设a<b<c,
现在的问题就是寻找整数a,b,c,
满足

由a<b<c,则有,
从而
 ,
,所以a2<24.又有
 ,
,所以a2>8,故a2=9或16.
若a2=9,则有
 ,
,由于
 ,并且
,并且 ,
,所以b2>72,72<b2<144.
故b2=81,100或121.将b2=81、100和121分别代入
 ,没有一个是完全平方数,
,没有一个是完全平方数,说明当a2=9时,
 无解.
无解.若a2=16,则
 .
.类似地,可得:16<b2<32,即b2=25,
此时,
 不是整数.
不是整数.综上所述,
 不能表示为3个互异的完全平方数的倒数之和.
不能表示为3个互异的完全平方数的倒数之和.评分参考:①正确回答第一问给(答案不唯一);
②能得到a2=9或16,给;
③能分别对a2=9和16讨论
 能否表示为3个互异的完全平方数的倒数之和,各给,共;
能否表示为3个互异的完全平方数的倒数之和,各给,共;④对代数式合理和正确的推导适当给分.
特别说明:因为各题的解答未必唯一,上述解答和评分仅供参考.
分析:(1)由
 证明即可;
证明即可;(2)设a<b<c,寻找满足
 的整数.
的整数.点评:此题利用分式的混合运算证明,难度较大,需要反复尝试.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
如图,一张边长为20cm正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无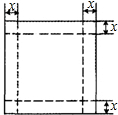 盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
(1)若用含有x的代数式表示V,则V=______.
(2)根据(1)中结果,填写下表:
| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V(cm3) | 324 | 512 | 500 | 384 | 252 |
(4)课后小英同学继续对这个问题作了以下探究:
当x=3.2cm时,V=591.872cm3;当x=3.3cm时,V=592.548cm3;
当x=3.4cm时,V=592.416cm3;当x=3.5cm时,V=591.5cm3,
小英同学发现x的取值一定介于3.3cm~3.4cm之间,估计x的取值还能更精确些,小英再计算x=3.3cm,3.33cm,3.333cm,3.3333cm…时,发现容积还在逐渐增大.现请你也观察(4)中数据变化,能否推测x可以取到哪一个定值,容积V的值最大?(直接写出即可)
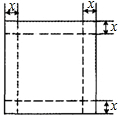 盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
盖的长方体,设长方体的容积为Vcm3,请回答下列问题:


