Question

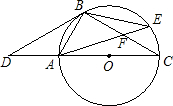如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且∠DBA=∠BCD．
（1）根据你的判断：BD是⊙O的切线吗？为什么？．
（2）若点E是劣弧BC上一点，AE与BC相交于点F，且△BEF的面积为10，cos∠BFA=

2

3

，那么，你能求出△ACF的面积吗？若能，请你求出其面积；若不能，请说明理由．

Answer 1

分析：（1）BD是⊙O的切线．先连接OB，由于AC是直径，那么∠ABC=90°，于是∠1+∠C=90°，而OA=OB，可得∠1=∠2，结合∠3=∠C，易得∠2+∠3=90°，从而可证DB是⊙O的切线；
（2）由于cos∠BFA=

2

3

，那么

BF

AF

=

2

3

，利用圆周角定理可知∠E=∠C，∠4=∠5，易证△EBF∽△CAF，于是

S△EBF

S△CFA

=(

BF

AF

) 2，从而易求△ACF的面积．

解答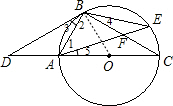：解：（1）BD是⊙O的切线．
理由：如右图所示，连接OB，
∵AC是⊙O的直径，
∴∠ABC=90°，
∴∠1+∠C=90°，
∵OA=OB，
∴∠1=∠2，
∴∠2+∠C=90°，
∵∠3=∠C，
∴∠2+∠3=90°，
∴DB是⊙O的切线；

（2）在Rt△ABF中，
∵cos∠BFA=

2

3

，
∴

BF

AF

=

2

3

，
∵∠E=∠C，∠4=∠5，
∴△EBF∽△CAF，
∴

S△EBF

S△CFA

=(

BF

AF

) 2，
即

10

S△ACF

=(

2

3

) 2，
解之得：S_△ACF=22.5．

点评：本题考查了切线的判定、相似三角形的判定和性质、圆周角定理、余弦．解题的关键是连接OB，并证明△EBF∽△CAF．