题目内容
已知抛物线y=-x2-2kx+3k2(k>0)交x轴于A、B两点,交y轴于点C,以AB为直径的⊙E交y轴于点D、F(如图),且DF=4,G是劣弧AD上的动点(不与点A、D重合),直线CG交x轴于点P.(1)求抛物线的解析式;
(2)当直线CG是⊙E的切线时,求tan∠PCO的值;
(3)当直线CG是⊙E的割线时,作GM⊥AB,垂足为H,交PF于点M,交⊙E于另一点N,设MN=t,GM=u,求u关于t的函数关系式.

分析:(1)本题抛物线解析式只有一个待定系数k,用k表示A、B两点坐标,用相交弦定理OA•OB=OD•OF,可求k值,确定抛物线解析式;
(2)由(1)可求圆的直径AB,半径EG及OC长,连接GE,由Rt△PGE∽Rt△POC,得出对应边的比相等,及切割线定理结合运用可求PA、PO长,在Rt△POC中,可求tan∠PCO的值.
(3)由GN∥CF,得相似,由中间比
=
=
,及GH=HN,CO=4,OF=2,得
=
,故HN=2HM,M为线段HN的中点,从而可得出:GM=3MN,即u=3t.
(2)由(1)可求圆的直径AB,半径EG及OC长,连接GE,由Rt△PGE∽Rt△POC,得出对应边的比相等,及切割线定理结合运用可求PA、PO长,在Rt△POC中,可求tan∠PCO的值.
(3)由GN∥CF,得相似,由中间比
| GH |
| CO |
| PH |
| PO |
| HM |
| OF |
| HN |
| 4 |
| HM |
| 2 |
解答:解:(1)解方程-x2-2kx+3k2=0.
得x1=-3k,x2=k.
由题意知OA=|-3k|=3k,OB=|k|=k.
∵直径AB⊥DF.
∴OD=OF=
DF=2.
∵OA•OB=OD•OF,
∴3k•k=2×2.
得k=±
(负的舍去).
则所求的抛物线的解析式为y=-x2-
x+4.
(2)由(1)可知AO=2
,AB=
,EG=
,
∵抛物线y=-x2-2kx+3k2过C点,∴OC=3k2=4.
连接EG,∵CG切⊙E于G,
∴∠PGE=∠POC=90°,
∴Rt△PGE∽Rt△POC.
∴
=
=
①,
由切割线定理得PG2=PA•PB=PA(PA+
),
PO=PA+AO=PA+2
.
代入①式整理得:
=
=
,
∴PA2+2
PA-6=0.
解得PA=3-
∵PA>0.
∴tan∠PCO=
=
.
(3)∵GN⊥AB,CF⊥AB,
∴GN∥CF,
∴△PGH∽△PCO,
∴
=
.
同理
=
.
∴
=
.
∵CO=4,OF=2,
∴HM=
GH=
HN=MN,
∴GM=3MN,
即u=3t(0<t≤
).
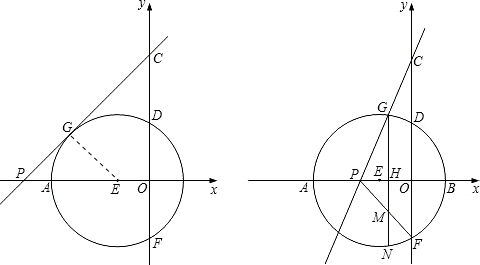
得x1=-3k,x2=k.
由题意知OA=|-3k|=3k,OB=|k|=k.
∵直径AB⊥DF.
∴OD=OF=
| 1 |
| 2 |
∵OA•OB=OD•OF,
∴3k•k=2×2.
得k=±
| 2 |
| 3 |
| 3 |
则所求的抛物线的解析式为y=-x2-
| 4 |
| 3 |
| 3 |
(2)由(1)可知AO=2
| 3 |
8
| ||
| 3 |
4
| ||
| 3 |
∵抛物线y=-x2-2kx+3k2过C点,∴OC=3k2=4.
连接EG,∵CG切⊙E于G,
∴∠PGE=∠POC=90°,
∴Rt△PGE∽Rt△POC.
∴
| PG |
| PO |
| EG |
| CO |
| ||
| 3 |

由切割线定理得PG2=PA•PB=PA(PA+
8
| ||
| 3 |
PO=PA+AO=PA+2
| 3 |
代入①式整理得:
| 1 |
| 3 |
| PG2 |
| PO 2 |
PA(PA+
| ||||
(PA+2
|
∴PA2+2
| 3 |
解得PA=3-
| 3 |
∵PA>0.
∴tan∠PCO=
| PA+AO |
| OC |
3+
| ||
| 4 |
(3)∵GN⊥AB,CF⊥AB,
∴GN∥CF,
∴△PGH∽△PCO,
∴
| GH |
| CO |
| PH |
| PO |
同理
| HM |
| OF |
| PH |
| PO |
∴
| GH |
| CO |
| HM |
| OF |
∵CO=4,OF=2,
∴HM=
| 1 |
| 2 |
| 1 |
| 2 |
∴GM=3MN,
即u=3t(0<t≤
2
| ||
| 3 |
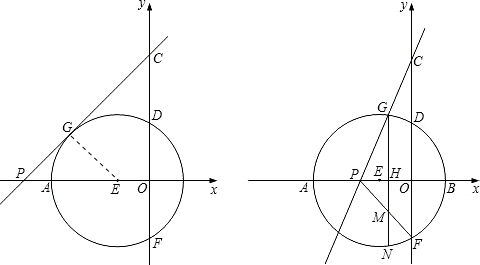
点评:本题综合性很强,涉及圆及切线性质,相交弦定理,切割线定理,利用相似三角形的中间比等知识,需要学生能熟练运用所学知识解答.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.