题目内容
 已知:如图,AD是⊙O的直径,BC是⊙O的弦,AD⊥BC,垂足为点E,BC=8,AD=10.
已知:如图,AD是⊙O的直径,BC是⊙O的弦,AD⊥BC,垂足为点E,BC=8,AD=10.
求:(1)OE的长;
(2)∠B的正弦值.
解:(1)连接OE,OB,如图所示:

∵直径AD=10,
∴AO=OB=OD=5,
又AD⊥BC,
∴E为BC的中点,又BC=8,
∴BE=CE= BC=4,
BC=4,
在Rt△BOE中,OB=5,BE=4,
根据勾股定理得:OE=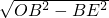 =3;
=3;
(2)∵AO=5,OE=3,
∴AE=AO+OE=5+3=8,
在Rt△ABE中,BE=4,AE=8,
根据勾股定理得:AB= =4
=4 ,
,
则sin∠ABC= =
= =
= .
.
分析:(1)连接OB,由直径AD垂直于弦BC,利用垂径定理得到E为BC的中点,同时由直径AD的长求出半径的长,再由BC的长求出BE的长,在直角三角形OBE中,利用勾股定理求出OE的长即可;
(2)由(1)求出的OE长,根据AO+OE求出AE的长,在直角三角形ABE中,利用勾股定理求出AB的长,最后利用锐角三角函数定义即可求出sin∠ABC的值.
点评:此题考查了垂径定理,勾股定理,以及锐角三角函数定义,熟练掌握定理是解本题的关键.

∵直径AD=10,
∴AO=OB=OD=5,
又AD⊥BC,
∴E为BC的中点,又BC=8,
∴BE=CE=
 BC=4,
BC=4,在Rt△BOE中,OB=5,BE=4,
根据勾股定理得:OE=
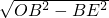 =3;
=3;(2)∵AO=5,OE=3,
∴AE=AO+OE=5+3=8,
在Rt△ABE中,BE=4,AE=8,
根据勾股定理得:AB=
 =4
=4 ,
,则sin∠ABC=
 =
= =
= .
.分析:(1)连接OB,由直径AD垂直于弦BC,利用垂径定理得到E为BC的中点,同时由直径AD的长求出半径的长,再由BC的长求出BE的长,在直角三角形OBE中,利用勾股定理求出OE的长即可;
(2)由(1)求出的OE长,根据AO+OE求出AE的长,在直角三角形ABE中,利用勾股定理求出AB的长,最后利用锐角三角函数定义即可求出sin∠ABC的值.
点评:此题考查了垂径定理,勾股定理,以及锐角三角函数定义,熟练掌握定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
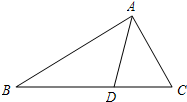 已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )| A、3:2 | B、9:4 | C、2:3 | D、4:9 |
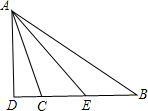 已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.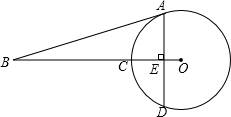
 已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.
已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF. 已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.