题目内容
已知如图，△ABC中，AD⊥BC于D，AC=BD=5，tan∠CAD=| 1 | 2 |
分析：根据题中所给的条件，在直角三角形中解题，知道正切值，在Rt△ADC中可以求出AD，然后在Rt△ADB中求AB．
解答：解：∵AD⊥BC，
△ADC为Rt△，又在Rt△ADC中
tan∠CAD=
=
，
∴设CD=xAD=2x，
由：CD2+AD2=AC2得
x2+4x2=25，
∵x＞0∴x=
，（3分）
∴在Rt△ADB中
AB=
=
=
=3
，（5分）
即AB长为3
．（6分）
△ADC为Rt△，又在Rt△ADC中
tan∠CAD=
| CD |
| AD |
| 1 |
| 2 |
∴设CD=xAD=2x，
由：CD2+AD2=AC2得
x2+4x2=25，
∵x＞0∴x=
| 5 |
∴在Rt△ADB中
AB=
| AD2+BD2 |
=
| 20+25 |
=
| 45 |
| 5 |
即AB长为3
| 5 |
点评：本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系，关键运用好两三角形的邻边．
练习册系列答案
阅读快车系列答案
相关题目
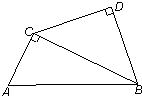已知如图，△ABC中，∠ACB=90°，△BCD中，∠D=90°，CD=BD，又AC=6，tan∠ABC=
7、已知如图，△ABC中，D在BC上，且∠1=∠2，请你在空白处填一个适当的条件：当
已知如图，△ABC中，BD⊥AC于D，tanA=
已知如图在△ABC中，∠ACB=90°，CD⊥AB于D，∠A的平分线交CD于F，BC于E，过点E作EH⊥AB于H．求证：EC=CF=EH．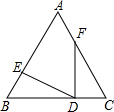
已知如图：△ABC中，AB=AC，BE=CD，BD=CF，则∠EDF=（ ）