题目内容
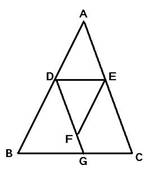
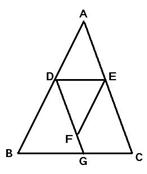
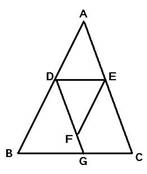
 25、如图,已知:∠BDG+∠EFG=180°,∠DEF=∠B.试判断∠AED与∠C的大小关系,并加以说明.
25、如图,已知:∠BDG+∠EFG=180°,∠DEF=∠B.试判断∠AED与∠C的大小关系,并加以说明.分析:先根据角平分线的定义得出∠EFD+∠EFG=180°,再由同角的补角相等及内错角相等,两直线平行可判断出BD∥EF,再根据两直线平行,同旁内角互补可得到∠BDE+∠DEF=180°,进而可判断出
DE∥BC,由平行线的性质即可得出答案.
DE∥BC,由平行线的性质即可得出答案.
解答:解:∠AED=∠C,理由如下:
∵∠EFD+∠EFG=180°,
∠BDG+∠EFG=180°,
∴∠BDG=∠EFD,
∴BD∥EF,
∴∠BDE+∠DEF=180°,
又∵∠DEF=∠B,
∴∠BDE+∠B=180°,
∴DE∥BC,
∴∠AED=∠C.
∵∠EFD+∠EFG=180°,
∠BDG+∠EFG=180°,
∴∠BDG=∠EFD,
∴BD∥EF,
∴∠BDE+∠DEF=180°,
又∵∠DEF=∠B,
∴∠BDE+∠B=180°,
∴DE∥BC,
∴∠AED=∠C.
点评:本题考查主要考查了平行线的判定与性质,熟知平行线得判定与性质的区别是解答此题的关键,即性质与判定的已知和结论正好相反,都是角的关系与平行线相关.

练习册系列答案
相关题目
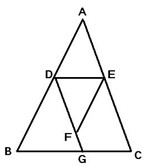 21、推理填空:
21、推理填空: