Question

已知：如图，抛物线y=-x²+bx+c与x轴、y轴分别相交于点A（-1，0）、B（0，3）两点，其顶点为D．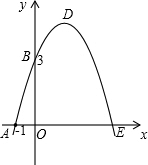
（1）求这条抛物线的解析式；
（2）若抛物线与x轴的另一个交点为E． 求△ODE的面积．
（注：抛物线y=ax²+bx+c（a≠0）的顶点坐标为（-

b

2a

，

4ac-b2

4a

）

Answer 1

分析：（1）由于抛物线的解析式中只有两个未知数，因此可根据A，B两点的坐标，用待定系数法求出抛物线的解析式．
（2）令y=0，求出抛物线与x轴的另一个交点坐标，再求出抛物线的顶点坐标，即为三角形ODE边OE上的高，根据三角形的面积公式求解即可．

解答：解：（1）由已知得：

c=3 -1-b+c=0

，
解得c=3，b=2，
∴抛物线的线的解析式为y=-x²+2x+3；

（2）令y=0，得-x²+2x+3=0，
解得x=-1或3，
∴E（3，0），
由顶点坐标公式得顶点坐标为（1，4），
S_△DOE=

1

2

×4×EO，
=

1

2

×3×4，
=6．

点评：本题考查了用待定系数法求二次函数的解析式、抛物线和x轴的交点问题，以及二次函数的性质，是基础知识要熟练掌握．