题目内容
已知二次函数的图象与x轴交于A(-2,0),B(3,0)两点,且函数有最大值2.
(1)求二次函数的函数关系式;
(2)设此二次函数图象的顶点为P,求△ABP的面积.
解:(1)∵该二次函数有最大值,
∴该函数的图象开口方向向下.
又∵二次函数的图象与x轴交于A(-2,0),B(3,0)两点,
∴该抛物线的对称轴是x= =
= ,函数有最大值2,
,函数有最大值2,
∴该函数的顶点是( ,2).
,2).
∴可设该二次函数解析式为y=a(x- )2+2(a<0),
)2+2(a<0),
则将点A的坐标代入,得0=a(-2- )2+2,解得a=-
)2+2,解得a=-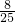 ,
,
∴二次函数的函数关系式y=-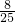 (x-
(x- )2+2;
)2+2;
(2)由(1)知,顶点P的坐标是( ,2).则点P到x轴的距离是2;
,2).则点P到x轴的距离是2;
由A(-2,0),B(3,0)知AB=5,
则S△ABP= ×5×2=5,即△ABP的面积是5.
×5×2=5,即△ABP的面积是5.
分析:(1)根据题意知该抛物线的顶点是( ,2),则可设该二次函数解析式为y=a(x-
,2),则可设该二次函数解析式为y=a(x- )2+2,然后将点A代入代入该解析式即可求得a的值;
)2+2,然后将点A代入代入该解析式即可求得a的值;
(2)根据三角形的面积公式来求△ABP的面积.
点评:本题考查了抛物线与x轴的交点.求二次函数解析式时,也可以设两点式方程y=a(x+2)(x-3)(a<0),然后把顶点坐标代入求得a值即可.
∴该函数的图象开口方向向下.
又∵二次函数的图象与x轴交于A(-2,0),B(3,0)两点,
∴该抛物线的对称轴是x=
 =
= ,函数有最大值2,
,函数有最大值2,∴该函数的顶点是(
 ,2).
,2).∴可设该二次函数解析式为y=a(x-
 )2+2(a<0),
)2+2(a<0),则将点A的坐标代入,得0=a(-2-
 )2+2,解得a=-
)2+2,解得a=-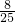 ,
,∴二次函数的函数关系式y=-
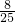 (x-
(x- )2+2;
)2+2;(2)由(1)知,顶点P的坐标是(
 ,2).则点P到x轴的距离是2;
,2).则点P到x轴的距离是2;由A(-2,0),B(3,0)知AB=5,
则S△ABP=
 ×5×2=5,即△ABP的面积是5.
×5×2=5,即△ABP的面积是5.分析:(1)根据题意知该抛物线的顶点是(
 ,2),则可设该二次函数解析式为y=a(x-
,2),则可设该二次函数解析式为y=a(x- )2+2,然后将点A代入代入该解析式即可求得a的值;
)2+2,然后将点A代入代入该解析式即可求得a的值;(2)根据三角形的面积公式来求△ABP的面积.
点评:本题考查了抛物线与x轴的交点.求二次函数解析式时,也可以设两点式方程y=a(x+2)(x-3)(a<0),然后把顶点坐标代入求得a值即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知二次函数的图象与y轴的交点坐标为(0,a),与x轴的交点坐标为(b,0)和(-b,0),若a>0,则函数解析式为( )
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
 已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.
已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.