题目内容
本题提供了两个备选题,请你从20-1和20-2题中任选一个予以解答,多做一个题不多计分.
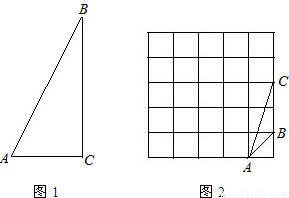
20-1.如图1,在△ACB中,∠ACB=90°.
(1)作线段AB的垂直平分线,交BC于点D;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)若AC=4,BC=8,求∠DAC的正切值.
20-2.知识链接:顶点都在网格线交点处的三角形叫做格点三角形.
如图2,己知格点△ABC.
①请在图中分别画出与△ABC相似且面积最大的格点△DEF.(要求:简述相似的理由)
②计算①中△DEF的面积.
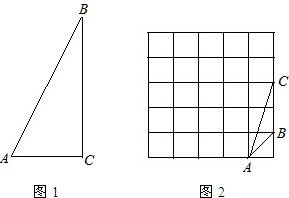
20-1.如图1,在△ACB中,∠ACB=90°.
(1)作线段AB的垂直平分线,交BC于点D;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)若AC=4,BC=8,求∠DAC的正切值.
20-2.知识链接:顶点都在网格线交点处的三角形叫做格点三角形.
如图2,己知格点△ABC.
①请在图中分别画出与△ABC相似且面积最大的格点△DEF.(要求:简述相似的理由)
②计算①中△DEF的面积.

分析:图1,(1)分别以点A、B为圆心,以任意长为半径画弧,两弧相交于两点,过这两点作直线交BC于点D,则点D即为所求;
(2)根据线段垂直平分线上的点到线段两端点的距离相等可得BD=AD,然后用CD表示出AD,在Rt△ACD中,利用勾股定理列式求出CD,再求出AD,然后根据正切=
列式计算即可得解;
图2,先利用网格结构根据勾股定理求出AB、BC、AC的长度,然后求出三边之比,再根据最长边与网格结构可以作出的三角形的最长边求出两三角形的相似比,利用网格结构作出△DEF即可,先求出△ABC的面积,然后根据相似三角形面积的比等于相似比的平方计算即可得解.
(2)根据线段垂直平分线上的点到线段两端点的距离相等可得BD=AD,然后用CD表示出AD,在Rt△ACD中,利用勾股定理列式求出CD,再求出AD,然后根据正切=
| 对边 |
| 邻边 |
图2,先利用网格结构根据勾股定理求出AB、BC、AC的长度,然后求出三边之比,再根据最长边与网格结构可以作出的三角形的最长边求出两三角形的相似比,利用网格结构作出△DEF即可,先求出△ABC的面积,然后根据相似三角形面积的比等于相似比的平方计算即可得解.
解答: 解:图1,(1)如图所示;
解:图1,(1)如图所示;
(2)∵点D是线段AB垂直平分线上的点,
∴AD=BD,
∵BC=8,
∴AD=BD=8-CD,
在Rt△ACD中,AD2=AC2+CD2,
即(8-CD)2=42+CD2,
解得CD=3,
所以tan∠DAC=
=
;
图2,①根据网格结构以及勾股定理,AB=
=
,
BC=2,AC=
=
,
所以三边之比为:
:2:
=1:
:
,
根据网格结构,可作三角形的最长边为
=5
,
所以△DEF和△ABC的相似比为5
:
=
,
其它两边分别为
,2
,
作图如图所示:
②S△ABC=
×2×1=1,
所以
=(
)2,
所以△DEF的面积=5×1=5.
 解:图1,(1)如图所示;
解:图1,(1)如图所示;(2)∵点D是线段AB垂直平分线上的点,
∴AD=BD,
∵BC=8,
∴AD=BD=8-CD,
在Rt△ACD中,AD2=AC2+CD2,
即(8-CD)2=42+CD2,
解得CD=3,
所以tan∠DAC=
| AC |
| CD |
| 4 |
| 3 |
图2,①根据网格结构以及勾股定理,AB=
| 12+12 |
| 2 |
BC=2,AC=
| 12+32 |
| 10 |
所以三边之比为:
| 2 |
| 10 |
| 2 |
| 5 |
根据网格结构,可作三角形的最长边为
| 52+52 |
| 2 |
所以△DEF和△ABC的相似比为5
| 2 |
| 10 |
| 5 |
其它两边分别为
| 10 |
| 5 |
作图如图所示:
②S△ABC=
| 1 |
| 2 |
所以
| △DEF的面积 |
| △ABC的面积 |
| 5 |
所以△DEF的面积=5×1=5.
点评:本题考查了利用相似变换作图,线段垂直平分线的作法,线段垂直平分线上的点到线段两端点的距离相等的性质,相似三角形面积的比等于相似比的性质,图2中根据最长边求出两三角形的相似比是作图的关键.

练习册系列答案
相关题目