Question

【题目】如图，在平面直角坐标系中A点的坐标为(8，) ，AB⊥轴于点B, sin∠OAB =，反比例函数的图象的一支经过AO的中点C，且与AB交于点D.

（1）求反比例函数解析式;

（2）求四边形OCDB的面积.

Answer 1

【答案】(1) y = ;(2)15.

【解析】（1）先根据锐角三角函数的定义，求出OA的值，然后根据勾股定理求出AB的值，然后由C点是OA的中点，求出C点的坐标，然后将C的坐标代入反比例函数中，即可确定反比例函数解析式；

（2）连接BC，分别求出△OMB的面积，△OBC的面积，△BCD的面积，进而确定四边形OCDB的面积．

解：(1) ∵A点的坐标为(8，m)，AB⊥x轴，

∴OB=8

∵Rt△OBA中，sin∠OAB =

∴OA = 8×= 10，AB == 6

∵C是OA的中点，且在第一象限 ∴C(4,3)

∴反比例函数的解析式为y =

(2)连接BC.

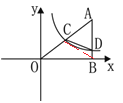
∵D在双曲线y=上，且D点横坐标为8

∴D (8，)，即BD=

又∵C(4,3)

∴四边形OCDB的面积

= ×8×3 + ××4

= 15