Question

如图，小蓓要赶上参观革命圣地的汽车，她从点A下发现汽车自点B处沿x轴向原点O方向匀速驶来，她立即从A处搭一辆摩托车，去截汽车．若点A的坐标为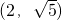，点B的坐标为（10，0），汽车行驶速度为摩托车速度的2倍，则小蓓最快截住汽车的坐标为

1. A.
   （3，0）
2. B.
   （3.5，0）
3. C.
   （4，0）
4. D.
   （5，0）

Answer 1

C
分析：在D点小蓓与汽车相遇，则小蓓的行进路线为AD，设OD=x，在直角△ACD中，AD为斜边，已知AC，CD，即可求AD，且BC=OB-OC=8，根据BD=2AD的等量关系可以求得x，即可求相遇点D的坐标．
解答：解：作出题目中给出的图形：
已知AC=，OC=2，OB=10，
在D点小蓓与汽车相遇，设OD=x，
则CD=x-2，
在直角△ACD中，AD为斜边，
则AD²=AC²+CD²，
AD=
∵OD=x，则BD=10-x，
存在10-x=2
解得：x=4，
故D点坐标（4，0）
故答案为C．
点评：本题考查了勾股定理在实际生活中的运用，考查了根据题意画出图形的能力，本题中找到汽车行驶速度为摩托车速度的2倍的等量关系，并且根据其求D点坐标是解题的关键．