题目内容
 如图,在正方形网格中,△ABC为格点三角形,每个小正方形的边长均为1个单位.
如图,在正方形网格中,△ABC为格点三角形,每个小正方形的边长均为1个单位.(1)画出△ABC关于y轴对称的三角形△A′B′C″;
(2)填空:△ABC中,AB长为
AC长为
(3)求AC边上的高.
分析:(1)以y轴为对称轴,直接画出△ABC的对称△A′B′C′即可;
(2)根据网格,由勾股定理求AB,BC,AC的值;
(3)已知△ABC的三边,由勾股定理的逆定理证明△ABC为直角三角形,利用“面积法”求斜边AC上的高.
(2)根据网格,由勾股定理求AB,BC,AC的值;
(3)已知△ABC的三边,由勾股定理的逆定理证明△ABC为直角三角形,利用“面积法”求斜边AC上的高.
解答: 解:(1)如图所示,三角形△A′B′C′为所求作;
解:(1)如图所示,三角形△A′B′C′为所求作;
(2)△ABC中,AB=
=3
,
BC=
=2
,
AC=
=
;
(3)∵AB2+BC2=(3
)2+(2
)2=26=AC2,
∴△ABC为直角三角形,
设AC边上的高为x,则有
AC•x=
AB•BC,
∴x=
=
.
 解:(1)如图所示,三角形△A′B′C′为所求作;
解:(1)如图所示,三角形△A′B′C′为所求作;(2)△ABC中,AB=
| 32+32 |
| 2 |
BC=
| 22+22 |
| 2 |
AC=
| 12+ 52 |
| 26 |
(3)∵AB2+BC2=(3
| 2 |
| 2 |
∴△ABC为直角三角形,
设AC边上的高为x,则有
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
3
| ||||
|
6
| ||
| 13 |
点评:本题考查了轴对称的作图,勾股定理的逆定理的运用.充分利用网格,构造直角三角形是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
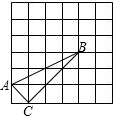 如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )
如图,在正方形网格中有△ABC,则sin∠ABC的值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
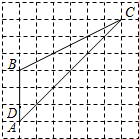 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE= 6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
6、如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
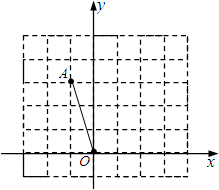 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).