题目内容
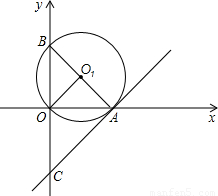
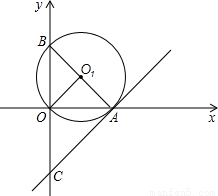
(2005•丰台区)在直角坐标系中,⊙O1经过坐标原点O,分别与x轴正半轴、y轴正半轴交于点A、B.(1)如图,过点A作⊙O1的切线与y轴交于点C,点O到直线AB的距离为
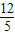 ,sin∠ABC=
,sin∠ABC= ,求直线AC的解析式;
,求直线AC的解析式;(2)若⊙O1经过点M(2,2),设△BOA的内切圆的直径为d,试判断d+AB的值是否会发生变化?如果不变,求出其值;如果变化,求其变化的范围.
【答案】分析:(1)过O作OG⊥AB于G,则OG= .根据三角函数分别求出A、C的坐标.利用待定系数法可求得直线AC的解析式为y=
.根据三角函数分别求出A、C的坐标.利用待定系数法可求得直线AC的解析式为y= x-
x- .
.
(2)设△AOB的内切圆分别切OA、OB、AB于点P、Q、T,则可求得BQ=BT=OB- ,AP=AT=OA-
,AP=AT=OA- ,AB=BT+AT=OB-
,AB=BT+AT=OB- +OA-
+OA- =OA+OB-d,则d+AB=d+OA+OB-d=OA+OB.
=OA+OB-d,则d+AB=d+OA+OB-d=OA+OB.
在x轴上取一点N,使AN=OB,连接OM、BM、AM、MN,求得△BOM≌△ANM,所以有OA+OB=OA+AN=ON= ×OM=
×OM= ×2
×2 =4,即d+AB的值不会发生变化,其值为4.
=4,即d+AB的值不会发生变化,其值为4.
解答: 解:(1)如图1,过O作OG⊥AB于G,则OG=
解:(1)如图1,过O作OG⊥AB于G,则OG= .
.
设OA=3k(k>0),
∵∠AOB=90°,sin∠ABC= .
.
∴AB=5k,OB=4k.
∵OA•OB=AB•OG=2S△AOB′
∴3k×4k=5× ,∴k=1.
,∴k=1.
∴OA=3,OB=4,AB=5,
∴A(3,0).
∵∠AOB=90°,
∴AB是⊙O1的直径.
∵AC切⊙O1于A,
∴BA⊥AC,∴∠BAC=90°.
在Rt△ABC中
∵cos∠ABC= ,
,
∴BC= .
.
∴OC=BC-OB= .
.
∴C(0,- ).
).
设直线AC的解析式为y=kx+b,则
∴ .
.
∴直线AC的解析式为y= x-
x- .
.
(2)结论:d+AB的值不会发生变化,
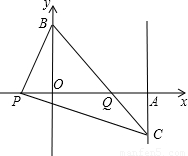
设△AOB的内切圆分别切OA、OB、AB于点P、Q、T,如图2所示.
∴BQ=BT,AP=AT,OQ=OP= .
.
∴BQ=BT=OB- ,AP=AT=OA-
,AP=AT=OA- .
.
∴AB=BT+AT=OB- +OA-
+OA- =OA+OB-d.
=OA+OB-d.
则d+AB=d+OA+OB-d=OA+OB.
在x轴上取一点N,使AN=OB,连接OM、BM、AM、MN.
∵M(2,2),
∴OM平分∠AOB,
∴OM=2 ,
,
∴∠BOM=∠MON=45°,
∴AM=BM,
又∵∠MAN=∠OBM,OB=AN,
∴△BOM≌△ANM,
∴∠BOM=∠ANM=45°,∠ANM=∠MON,
∴OM=NM∠OMN=90°,
∴OA+OB=OA+AN=ON= ×OM=
×OM= ×2
×2 =4.
=4.
∴d+AB的值不会发生变化,其值为4.
点评:主要考查了一次函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.
 .根据三角函数分别求出A、C的坐标.利用待定系数法可求得直线AC的解析式为y=
.根据三角函数分别求出A、C的坐标.利用待定系数法可求得直线AC的解析式为y= x-
x- .
.(2)设△AOB的内切圆分别切OA、OB、AB于点P、Q、T,则可求得BQ=BT=OB-
 ,AP=AT=OA-
,AP=AT=OA- ,AB=BT+AT=OB-
,AB=BT+AT=OB- +OA-
+OA- =OA+OB-d,则d+AB=d+OA+OB-d=OA+OB.
=OA+OB-d,则d+AB=d+OA+OB-d=OA+OB.在x轴上取一点N,使AN=OB,连接OM、BM、AM、MN,求得△BOM≌△ANM,所以有OA+OB=OA+AN=ON=
 ×OM=
×OM= ×2
×2 =4,即d+AB的值不会发生变化,其值为4.
=4,即d+AB的值不会发生变化,其值为4.解答:
 解:(1)如图1,过O作OG⊥AB于G,则OG=
解:(1)如图1,过O作OG⊥AB于G,则OG= .
.设OA=3k(k>0),
∵∠AOB=90°,sin∠ABC=
 .
.∴AB=5k,OB=4k.
∵OA•OB=AB•OG=2S△AOB′
∴3k×4k=5×
 ,∴k=1.
,∴k=1.∴OA=3,OB=4,AB=5,
∴A(3,0).
∵∠AOB=90°,
∴AB是⊙O1的直径.
∵AC切⊙O1于A,
∴BA⊥AC,∴∠BAC=90°.
在Rt△ABC中
∵cos∠ABC=
 ,
,∴BC=
 .
.∴OC=BC-OB=
 .
.∴C(0,-
 ).
).设直线AC的解析式为y=kx+b,则

∴
 .
.∴直线AC的解析式为y=
 x-
x- .
.(2)结论:d+AB的值不会发生变化,
设△AOB的内切圆分别切OA、OB、AB于点P、Q、T,如图2所示.
∴BQ=BT,AP=AT,OQ=OP=
 .
.∴BQ=BT=OB-
 ,AP=AT=OA-
,AP=AT=OA- .
.
∴AB=BT+AT=OB-
 +OA-
+OA- =OA+OB-d.
=OA+OB-d.则d+AB=d+OA+OB-d=OA+OB.
在x轴上取一点N,使AN=OB,连接OM、BM、AM、MN.
∵M(2,2),
∴OM平分∠AOB,
∴OM=2
 ,
,∴∠BOM=∠MON=45°,
∴AM=BM,
又∵∠MAN=∠OBM,OB=AN,
∴△BOM≌△ANM,
∴∠BOM=∠ANM=45°,∠ANM=∠MON,
∴OM=NM∠OMN=90°,
∴OA+OB=OA+AN=ON=
 ×OM=
×OM= ×2
×2 =4.
=4.∴d+AB的值不会发生变化,其值为4.
点评:主要考查了一次函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
相关题目
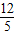 ,sin∠ABC=
,sin∠ABC= ,求直线AC的解析式;
,求直线AC的解析式;