��Ŀ����
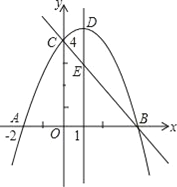
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA=4��OC=3���Ҷ���A��C�����������ϣ�����M�ӵ�A��������ÿ��1����λ���ȵ��ٶ���AO���յ�O�ƶ�����N�ӵ�C������CB���յ�B��ͬ�����ٶ��ƶ��������������˶���x�루0��x��4��ʱ������N��NP��BC��BO�ڵ�P������MP��
��1��ֱ��д����B�����꣬�������P�����꣨�ú�x��ʽ�ӱ�ʾ����
��2������OMP�����ΪS����S��x֮��ĺ�������ʽ�����������ֵ�����S�����ֵ��
��3�������������˶��Ĺ����У��Ƿ����ijһʱ�̣�ʹ��OMP�ǵ��������Σ������ڣ����x��ֵ���������ڣ���˵�����ɣ�
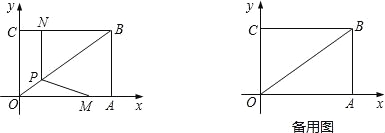
���𰸡���1��B��4��3����P��x��![]() x������2��S=��
x������2��S=��![]() x2+
x2+![]() x��0��x��4��, ���ֵΪ
x��0��x��4��, ���ֵΪ![]() ����3�����ڣ�x��ֵΪ
����3�����ڣ�x��ֵΪ![]() ���
���![]() ���
���![]() ��.
��.
��������
�����������1�����ݾ���OABC��OA=4��OC=3�Լ����ε����ʣ��ó�B�����꣬����PG��AB���ó���OPG�ס�OBA���������������ζ�Ӧ�߳ɱ����ó�P�����ꣻ��2������PG�Լ�OM�ij���ʾ����OMP��������ٸ��ݶ��κ���������������ֵ���ɣ���3����OMP�ǵ���������ʱ���������������PO=PM����OP=OM����OM=PM������ͼ�Σ��ֱ�������ɣ�
�����������1��������OABC�У�OA=4��OC=3����B������Ϊ��4��3������ͼ���ӳ�NP����OA�ڵ�G����PG��AB��OG=CN=x����PG��AB�����OPG�ס�OBA����![]() ����
����![]() =
=![]() ����ã�PG=
����ã�PG=![]() x������P������Ϊ��x��
x������P������Ϊ��x��![]() x������2��������OMP�У�OM=4��x��OM���ϵĸ�Ϊ
x������2��������OMP�У�OM=4��x��OM���ϵĸ�Ϊ![]() x����S=
x����S=![]() ��4��x��
��4��x��![]() x=��
x=��![]() x2+
x2+![]() x����S��x֮��ĺ�������ʽΪS=��
x����S��x֮��ĺ�������ʽΪS=��![]() x2+
x2+![]() x��0��x��4�����䷽����S=��
x��0��x��4�����䷽����S=��![]() ��x��2��2+
��x��2��2+![]() ������x=2ʱ��S�����ֵ�����ֵΪ
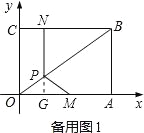
������x=2ʱ��S�����ֵ�����ֵΪ![]() ����3������ijһʱ�̣�ʹ��OMP�ǵ��������Σ��������£����籸��ͼ1������P��PG��AO�ڵ�G����PO=PM����OG=GM=CN=x����3x=4����ã�x=
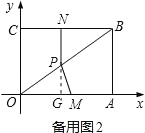
����3������ijһʱ�̣�ʹ��OMP�ǵ��������Σ��������£����籸��ͼ1������P��PG��AO�ڵ�G����PO=PM����OG=GM=CN=x����3x=4����ã�x=![]() �����籸��ͼ2������P��PG��AO�ڵ�G����OP=OM��CN=x����OP= OM= 4��x���ɹ��ɶ�������OB=
�����籸��ͼ2������P��PG��AO�ڵ�G����OP=OM��CN=x����OP= OM= 4��x���ɹ��ɶ�������OB=![]() =
=![]() =5����NP��OC����
=5����NP��OC����![]() ����
����![]() ����OP=
����OP=![]() x����
x����![]() x=4��x����ã�x=
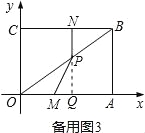
x=4��x����ã�x=![]() �����籸��ͼ3������P��PQ��OA������ΪQ����OM=PMʱ����PM=OM=4��x��OQ=CN=x����MQ=x-(4-x)=2x��4����Rt��MPQ�У�PQ2+QM2=MP2������
�����籸��ͼ3������P��PQ��OA������ΪQ����OM=PMʱ����PM=OM=4��x��OQ=CN=x����MQ=x-(4-x)=2x��4����Rt��MPQ�У�PQ2+QM2=MP2������![]() x��2+��2x��4��2=��4��x��2����ã�x=
x��2+��2x��4��2=��4��x��2����ã�x=![]() ��������������x��ֵΪ
��������������x��ֵΪ![]() ���
���![]() ���
���![]() ��ʱ����OMP�ǵ��������Σ�
��ʱ����OMP�ǵ��������Σ�


 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д�