题目内容
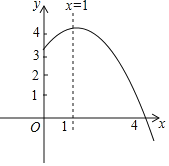
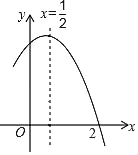
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(
,且经过点(2,0),下列说法:①abc<0;②﹣2b+c=0;③4a+2b+c<0;④若(![]() ,y1)、(
,y1)、(![]() ,y2)是抛物线上的两点,则y1<y2;⑤
,y2)是抛物线上的两点,则y1<y2;⑤![]() >m(am+b)(其中m≠
>m(am+b)(其中m≠![]() ).其中说法正确的是_____
).其中说法正确的是_____
【答案】①②④⑤;
【解析】
①根据抛物线开口方向、对称轴位置、抛物线与y轴交点位置求得a、b、c的符号②根据对称轴求出b=﹣a;③把x=2代入函数关系式,结合图象判断函数值与0的大小关系;④求出点(-![]() ,y1)关于直线x=
,y1)关于直线x=![]() 的对称点的坐标,根据对称轴即可判断y1和y2的大小,⑤根据最大值判断即可.
的对称点的坐标,根据对称轴即可判断y1和y2的大小,⑤根据最大值判断即可.
①∵图像开口向下,
∴a<0,
∵抛物线与y轴交于y轴正半轴,
∴c>0,
∵对称轴x= -![]() =
=![]() >0,
>0,
∴b>0,
∴abc<0,故①正确;
②将(2,0)代入y=ax2+bx+c (a≠0),
得4a+2b+c=0,
∵-![]() =
=![]() ,
,
∴a=﹣b,
∴﹣4b+2b+c=0,
∴﹣2b+c=0,故②正确;
③由②可知:4a+2b+c=0,故③错误;
④由于抛物线的对称轴为x=![]() ,
,
∴(![]() ,y1)与(
,y1)与(![]() ,y1)关于x=
,y1)关于x=![]() 对称,
对称,
∵由于x>![]() 时,y随着x的增大而减小,
时,y随着x的增大而减小,![]() >
>![]() ,
,
∴y1<y2 ,故④正确;
⑤由图象可知:x=![]() 时,y可取得最大值,且最大值为
时,y可取得最大值,且最大值为![]() a+
a+![]() b+c,
b+c,
∴m≠![]()
∴ a+ b+c>am2+bm+c,
∴![]() a+
a+![]() b>m(am+b),故⑤正确;
b>m(am+b),故⑤正确;
故答案为:①②④⑤;

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
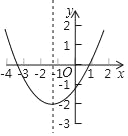
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;