题目内容
如图,点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=| 2 | 3 |

分析:可证明△ACF∽△BEF,再由直径所对的圆周角等于90°,得出△BFA为直角三角形,由余弦的定义得出
=
,再根据相似三角形的面积之比等于相似比的平方,求出△ACF的面积即可.
| BF |
| AF |
| 2 |
| 3 |
解答:解:∵∠C=∠E,∠CAF=∠EBF,
∴△ACF∽△BEF,(2分)
∵AC是⊙O的直径,
∴∠ABC=90°,(4分)
在Rt△BFA中,cos∠BFA=
=
,(5分)
∴
=(
)2=
,(6分)
又∵S△BEF=8,
∴S△ACF=18.(8分)
∴△ACF∽△BEF,(2分)
∵AC是⊙O的直径,
∴∠ABC=90°,(4分)
在Rt△BFA中,cos∠BFA=
| BF |
| AF |
| 2 |
| 3 |
∴
| S△BEF |
| S△ACF |
| BF |
| AF |
| 4 |
| 9 |
又∵S△BEF=8,
∴S△ACF=18.(8分)
点评:本题考查了相似三角形的判定和性质,圆周角定理以及解直角三角形,注:相似三角形的面积之比等于相似比的平方.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.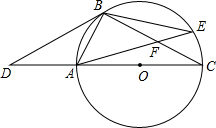 如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
 ,求△ACF的面积.
,求△ACF的面积.
 ,求△ACF的面积.
,求△ACF的面积.