题目内容
如果a+
ab+b=
，且b是有理数，那么（ ）
| 2 |
| 2 |
| A、a是整数 |
| B、a是有理数 |
| C、a是无理数 |
| D、a可能是有理数，也可能是无理数 |
分析：先把等式变形为a+b=
（1-ab），再根据等式一边出现无理数则a，b中必有一个数为无理数即可进行解答．
| 2 |
解答：解：∵a+
ab+b=
，
∴a+b=
（1-ab）
等式一边出现无理数，若a，b均为有理数，则等式恒不成立，
又∵b为有理数，
∴a必为无理数．
故选C．
| 2 |
| 2 |
∴a+b=
| 2 |
等式一边出现无理数，若a，b均为有理数，则等式恒不成立，
又∵b为有理数，
∴a必为无理数．
故选C．
点评：本题考查的是有理数及无理数的概念及运算，能把原式化为a+b=
（1-ab）的形式是解答此题的关键．
| 2 |
练习册系列答案
相关题目
如图，△ABC中，点D、E分别是边BC、AC的中点，过点A作AF∥BC交线段DE的延长线相交于F点，取AF的中点G，如果BC=2AB．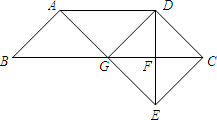
（2013•闵行区二模）已知：如图，在梯形ABCD中，AD∥BC，AB=CD，BC=2AD．DE⊥BC，垂足为点F，且F是DE的中点，联结AE，交边BC于点G．