Question

已知二次函数y=-x²+4x+5图象交x轴于点A、B，交y轴于点C，点D是该函数图象上一点，且点D的横坐标为4，连BD，点P是AB上一动点（不与点A重合），过P作PQ⊥AB交射线AD于点Q，以PQ为一边在PQ的右侧作正方形PQMN．设点P的坐标为（t，0）．
（1）求点B，C，D的坐标及射线AD的解析式；
（2）在AB上是否存在点P，使△OCM为等腰三角形？若存在，求正方形PQMN 的边长；若不存在，请说明理由；
（3）设正方形PQMN与△ABD重叠部分面积为s，求s与t的函数关系式．

Answer 1

解：（1）当x=0时，y=5，则C点坐标为（0，5），
当y=0时，-x²+4x+5=0，
解得（x+1）（x-5）=0，
x₁=-1；x₂=5．
则A点坐标为（-1，0），B点坐标为（5，0）．
将x=4代入y=-x²+4x+5得，y=-16+16+5=5，
则D点坐标为（4，5）．
设AD的解析式为y=kx+b，
把A（-1，0），D（4，5）分别代入解析式y=kx+b得，
，
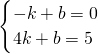解得，
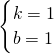函数解析式为y=x+1（x≥-1）．

（2）∵直线AD的解析式为：y=x+1，且P（t，0）．
∴Q（t，t+1），M（2t+1，t+1）
当MC=MO时：t+1=，
∴边长为．…
当OC=OM时：（2t+1）²+（t+1）²=5²
解得（舍去），
∴边长为t+1=．…
当CO=CM时：（2t+1）²+（4-t）²=5²
解得，．
∴边长为t+1=．
或t+1=…

（3）当1＜t≤时，正方形的边长为（t+1），故其面积为：s=（t+1）²；…
当时：；…
当2≤t≤4时：；…
当4≤t≤5时：．…
分析：（1）根据二次函数解析式，当x=0时，求出C点坐标；当y=0时，求出B点坐标及点A坐标；将D点横坐标代入y=-x²+4x+5，即可求出点D纵坐标；根据点A、点D坐标，应用待定系数法即可求出射线AD解析式；
（2）假设存在点P，使△OCM为等腰三角形，根据勾股定理，若能求出P点坐标，则P存在，同时可求出正方形PQMN 的边长；否则P不存在；
（3）由于重叠部分面积是不确定的，所以要根据其重叠程度，分情况讨论，得到不同的表达式．
点评：本题考查了二次函数的图象和性质、待定系数法求一次函数解析式、三角形及正方形的性质、存在性问题等内容，综合性强，属于难题．