题目内容
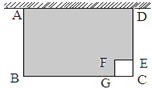
【题目】如图,△ABC中,∠ABC=90°,AB=2,BC=4,现将△ABC绕顶点B顺时针方向旋转△A′BC′的位置,此时A′C′与BC的交点D是BC的中点,则线段C′D的长度是( ) 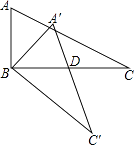
A.![]()
B.![]()
C.![]()
D.2 ![]()
【答案】B
【解析】解:过点B作BM⊥A′C′,交A′C′于点M,如图所示: 
∵∠ABC=90°,AB=2,BC=4,
∴AC= ![]() =
= ![]() =2
=2 ![]() ,cosA=
,cosA= ![]() =
= ![]() =
= ![]() ,
,
由题意得:∠A′=∠A,A′B=AB=2,A′C′=AC=2 ![]() ,
,
∵点D为BC的中点,
∴BD= ![]() BC=2,BD=A′B,而BM⊥A′C′,
BC=2,BD=A′B,而BM⊥A′C′,
∴A′M=DM,
∵cosA′=cosA,且cosA′= ![]() ,
,
∴A′M= ![]() ×2=
×2= ![]() ,
,
∴C'D=A'C'﹣2A'M=2 ![]() ﹣2×
﹣2× ![]() =
= ![]() ,
,
所以答案是:B.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目