题目内容
P是凸四边形内的一点,P与四个顶点连接得到的四条线段的长分别为1,2,3,4.那么,这个四边形的面积的最大值为
- A.10.5
- B.12
- C.12.5
- D.15
C
分析:首先讨论当两边a、b一定时,要是三角形的面积最大,必须两边的夹角最大,即是直角时,由此得到AC⊥BD,分别求出所有的情况,找出最大值即可.
解答: 解:图(1)中,设△EFG的边FG=a、EG=b,过E作EH⊥FG于H,
解:图(1)中,设△EFG的边FG=a、EG=b,过E作EH⊥FG于H,
sinG= ,
,
∴EH=bsinG,
S△EFG= •FG•EH=
•FG•EH= absinG,
absinG,
要是△EFG的面积最大,当a、b一定时,sinG最大,
即sinG=1,即∠G=90°.
同理:连接PA、PB、PC、PD,
∵S四边形ABCD=S△PAB+S△PBC+S△PCD+S△PAD,
要是四边形ABCD的面积最大,必须△PAB、△PBC、△PCD、△PAD的面积最大,
由上面证明可知当两边一定时,两边的夹角是直角时面积最大,
即AC⊥BD时面积最大,
有下面三种情况:
(1)当BD=1+2=3,AC=3+4=7时,S= ×3×7=10.5;
×3×7=10.5;
(2)当BD=1+4=5,AC=2+3=5时,S= ×5×5=12.5;
×5×5=12.5;
(3)当BD=1+3=4,AC=2+4=6时,S= ×4×6=12;
×4×6=12;
∴四边形ABCD的面积的最大值是12.5.
故选C.
点评:本题主要考查了面积及等积变换,三角形的面积公式,解此题的关键是得出当两边一定时,两边的夹角是90°时,三角形的面积最大的结论.
分析:首先讨论当两边a、b一定时,要是三角形的面积最大,必须两边的夹角最大,即是直角时,由此得到AC⊥BD,分别求出所有的情况,找出最大值即可.
解答:
 解:图(1)中,设△EFG的边FG=a、EG=b,过E作EH⊥FG于H,
解:图(1)中,设△EFG的边FG=a、EG=b,过E作EH⊥FG于H,sinG=
 ,
,∴EH=bsinG,
S△EFG=
 •FG•EH=
•FG•EH= absinG,
absinG,要是△EFG的面积最大,当a、b一定时,sinG最大,
即sinG=1,即∠G=90°.
同理:连接PA、PB、PC、PD,
∵S四边形ABCD=S△PAB+S△PBC+S△PCD+S△PAD,
要是四边形ABCD的面积最大,必须△PAB、△PBC、△PCD、△PAD的面积最大,
由上面证明可知当两边一定时,两边的夹角是直角时面积最大,
即AC⊥BD时面积最大,
有下面三种情况:
(1)当BD=1+2=3,AC=3+4=7时,S=
 ×3×7=10.5;
×3×7=10.5;(2)当BD=1+4=5,AC=2+3=5时,S=
 ×5×5=12.5;
×5×5=12.5;(3)当BD=1+3=4,AC=2+4=6时,S=
 ×4×6=12;
×4×6=12;∴四边形ABCD的面积的最大值是12.5.
故选C.
点评:本题主要考查了面积及等积变换,三角形的面积公式,解此题的关键是得出当两边一定时,两边的夹角是90°时,三角形的面积最大的结论.

练习册系列答案
相关题目
P是凸四边形内的一点,P与四个顶点连接得到的四条线段的长分别为1,2,3,4.那么,这个四边形的面积的最大值为( )
| A、10.5 | B、12 | C、12.5 | D、15 |
 如图,设P是凸四边形ABCD内的一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1.则四边形ABCD的周长为
如图,设P是凸四边形ABCD内的一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1.则四边形ABCD的周长为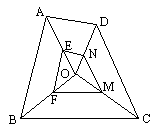
 如图,设P是凸四边形ABCD内的一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1.则四边形ABCD的周长为________.
如图,设P是凸四边形ABCD内的一点,过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H.已知AH=3,HD=4,DG=1,GC=5,CF=6,FB=4,且BE-AE=1.则四边形ABCD的周长为________.