题目内容
已知:二次函数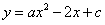 的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=1,且图象向右平移一个单位后经过坐标原点O。
的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=1,且图象向右平移一个单位后经过坐标原点O。
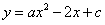 的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=1,且图象向右平移一个单位后经过坐标原点O。
的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴是直线x=1,且图象向右平移一个单位后经过坐标原点O。 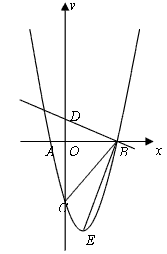
(1)求这个二次函数的解析式;
(2)直线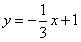 交y轴于D点,E为抛物线顶点。若
交y轴于D点,E为抛物线顶点。若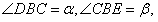 求
求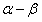 的值;
的值;
(3)在(2)问的前提下,P为抛物线对称轴上一点,且满足PA=PC,在y轴右侧的抛物线上是否存在点M,使得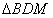 的面积等于PA2,若存在,求出点M的坐标;若不存在,请说明理由。
的面积等于PA2,若存在,求出点M的坐标;若不存在,请说明理由。
(2)直线
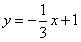 交y轴于D点,E为抛物线顶点。若
交y轴于D点,E为抛物线顶点。若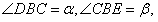 求
求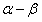 的值;
的值;(3)在(2)问的前提下,P为抛物线对称轴上一点,且满足PA=PC,在y轴右侧的抛物线上是否存在点M,使得
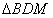 的面积等于PA2,若存在,求出点M的坐标;若不存在,请说明理由。
的面积等于PA2,若存在,求出点M的坐标;若不存在,请说明理由。 解:(1)由题意, ∵对称轴是直线x=1 ∴  把  , , 分别代入 分别代入 得 得 解得  ∴这个二次函数的解析式为  ; ;(2)直线  与y轴交于 与y轴交于 ,∴ ,∴  由  得 得    ∴  ∴△BOD∽△BCE ∴  ∴  (3)设   ∴  即 即 解得n=-1 ∴  ∴  设存在符合条件的点  则m>0 则m>0 ①当M在直线BD上侧时,连接OM(如图1), 则  即   整理,得  解得  (舍去), (舍去),  把  代入 代入 得 得  ∴  ②当M在直线BD下侧时,不妨叫M1连接OM1(如图1), 则  即   整理,得  解得  (舍去) (舍去) 把m=2代入  得y=-3 得y=-3 ∴  综上所述,存在符合条件的点M其坐标为  或 或 |
 |

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目