题目内容
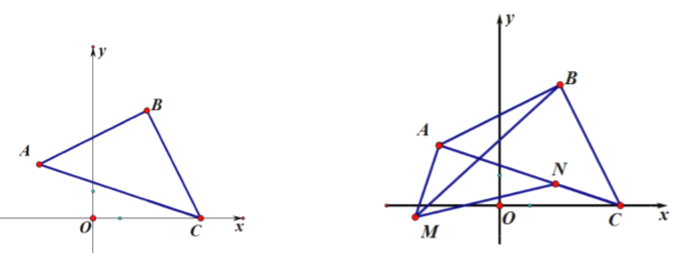
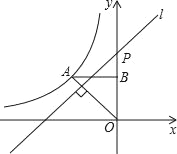
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据反比例函数图象上点的坐标特征由A点坐标为(﹣2,2)得到k=﹣4,即反比例函数解析式为y=﹣![]() ,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(﹣
,且OB=AB=2,则可判断△OAB为等腰直角三角形,所以∠AOB=45°,再利用PQ⊥OA可得到∠OPQ=45°,然后轴对称的性质得PB=PB′,BB′⊥PQ,所以∠BPQ=∠B′PQ=45°,于是得到B′P⊥y轴,则点B′的坐标可表示为(﹣![]() ,t),于是利用PB=PB′得t﹣2=|﹣
,t),于是利用PB=PB′得t﹣2=|﹣![]() |=
|=![]() ,然后解方程可得到满足条件的t的值.
,然后解方程可得到满足条件的t的值.
如图,∵点A坐标为(﹣2,2),
∴k=﹣2×2=﹣4,
∴反比例函数解析式为y=﹣![]() ,
,
∵OB=AB=2,
∴△OAB为等腰直角三角形,
∴∠AOB=45°,
∵PQ⊥OA,
∴∠OPQ=45°,
∵点B和点B′关于直线l对称,
∴PB=PB′,BB′⊥PQ,
∴∠B′PQ=∠OPQ=45°,∠B′PB=90°,
∴B′P⊥y轴,
∴点B′的坐标为(﹣![]() ,t),
,t),
∵PB=PB′,
∴t﹣2=|﹣![]() |=
|=![]() ,
,
整理得t2﹣2t﹣4=0,解得t1=1+![]() ,t2=1﹣
,t2=1﹣![]() (不符合题意,舍去),
(不符合题意,舍去),
∴t的值为1+![]() ,
,
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目