题目内容
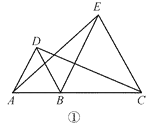
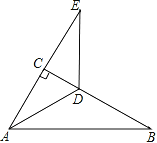
【题目】在△ABC中，∠ABC=45°，tan∠ACB= 
．如图，把△ABC的一边BC放置在x轴上，有OB=14，OC= 
，AC与y轴交于点E．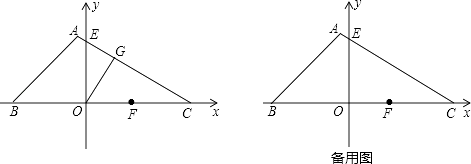
（1）求AC所在直线的函数解析式；
（2）过点O作OG⊥AC，垂足为G，求△OEG的面积；
（3）已知点F（10，0），在△ABC的边上取两点P，Q，是否存在以O，P，Q为顶点的三角形与△OFP全等，且这两个三角形在OP的异侧？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
【答案】
（1）
解：在Rt△OCE中，OE=OCtan∠OCE= 
=2 
，∴点E（0，2 ）．
设直线AC的函数解析式为y=kx+2 ，有 
，解得：k=- 
．
∴直线AC的函数解析式为y= 
（2）
解：在Rt△OGE中，tan∠EOG=tan∠OCE= 
= ，
设EG=3t，OG=5t，OE= 
= t，∴ 
，得t=2，
故EG=6，OG=10，
∴S△OEG= 
（3）
解：存在．
①当点Q在AC上时，点Q即为点G，
如图1，作∠FOQ的角平分线交CE于点P1，
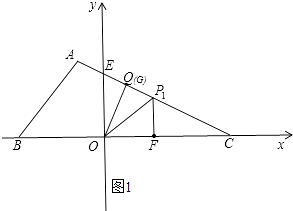
由△OP1F≌△OP1Q，则有P1F⊥x轴，由于点P1在直线AC上，当x=10时，
y=﹣ 
= 
，
∴点P1（10， ）．
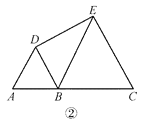
②当点Q在AB上时，
如图2，有OQ=OF，作∠FOQ的角平分线交CE于点P2，
过点Q作QH⊥OB于点H，设OH=a，
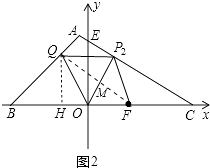
则BH=QH=14﹣a，
在Rt△OQH中，a2+（14﹣a）2=100，
解得：a1=6，a2=8，
∴Q（﹣6，8）或Q（﹣8，6）．
连接QF交OP2于点M．
当Q（﹣6，8）时，则点M（2，4）．
当Q（﹣8，6）时，则点M（1，3）．
设直线OP2的解析式为y=kx，则
2k=4，k=2．
∴y=2x．
解方程组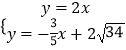 
，得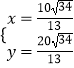 
．
∴P2（ 
）；
当Q（﹣8，6）时，则点M（1，3），
同理可求P3（ 
）；
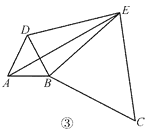
如图4，由QP4∥OF，QP4=OF=10，
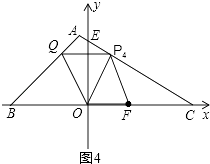
设点P4的横坐标为x，则点Q的横坐标为（x﹣10），
∵yQ=yP，直线AB的函数解析式为：y=x+14，
∴x﹣10+14=﹣ x+2 ，
解得：x= 
，可得y= 
，
∴点P4（ ， ），
③当Q在BC边上时，如图5，OQ=OF=10，点P5在E点，
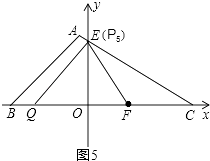
∴P5（0，2 ），
综上所述，满足条件的P点坐标为（10， ）或（ ）或（ ）或（0，2 ），（ ， ）．
【解析】（1）根据三角函数求E点坐标，运用待定系数法求解；（2）在Rt△OGE中，运用三角函数和勾股定理求EG，OG的长度，再计算面积；（3）分两种情况讨论求解：①点Q在AC上；②点Q在AB上③当Q在BC边上时．求直线OP与直线AC的交点坐标即可．
【考点精析】认真审题，首先需要了解二次函数的性质(增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小)．
