题目内容
(2005•扬州)为了配合数学课程改革,某县举行了初三年级“数学知识应用”竞赛(满分100分).为了解初三年级参赛的1万名学生竞赛成绩情况,现从中随机抽取部分学生的竞赛成绩作为一个样本,整理后分成5组,绘制出频数分布直方图.已知图中从左到右的第一、第二、第四、第五小组的频数分别是50,100,200,25,其中第二小组的频率是0.2.(1)求第三小组的频数,并补全频数分布直方图;
(2)抽取的样本中,学生竞赛成绩的中位数落在第几小组?
(3)若成绩在90分以上(含90分)的学生获优胜奖,请你估计全县初三参赛学生中获优胜奖的人数.

【答案】分析:(1)总数是100÷0.2=500,所以第三组的频数是125,画图即可;
(2)根据中位数的求算方法可知中位数落在第三组;
(3)用样本来估计总体.
解答:解:
(1)样本容量=100÷2=500,则第三小组的频数=500-50-100-200-25=125,补图
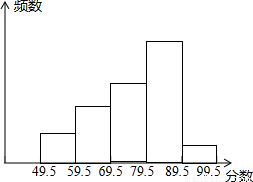
(2)因为中位数是从小到大排列的第250,第251这两个数据和的平均数,
又因为落在前三小组的频数分别为50,100,125
所以抽取的样本中的中位数落在第三小组;
(3)因为10000×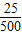 =500,
=500,
所以估计全县初三参赛学生中获优胜奖的有500人.
点评:主要考查了频率的计算方法和如何画频率分布折线图,还考查了中位数的确定方法和用样本估计总体的能力.
(2)根据中位数的求算方法可知中位数落在第三组;
(3)用样本来估计总体.
解答:解:
(1)样本容量=100÷2=500,则第三小组的频数=500-50-100-200-25=125,补图

(2)因为中位数是从小到大排列的第250,第251这两个数据和的平均数,
又因为落在前三小组的频数分别为50,100,125
所以抽取的样本中的中位数落在第三小组;
(3)因为10000×
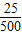 =500,
=500,所以估计全县初三参赛学生中获优胜奖的有500人.
点评:主要考查了频率的计算方法和如何画频率分布折线图,还考查了中位数的确定方法和用样本估计总体的能力.

练习册系列答案
相关题目
(2005•扬州)为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
解答下列问题:
(1)在这个问题中,总体是______,样本容量a=______;
(2)第四小组的频率c=______;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 60 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 | |
(1)在这个问题中,总体是______,样本容量a=______;
(2)第四小组的频率c=______;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
(2005•扬州)为配和新课程的实施,某市举行了“应用与创新”知识竞赛,共有1万名学生参加了这次竞赛(满分100分,得分全为整数).为了解本次竞赛成绩情况,从中随机抽取了部分学生的竞赛成绩,进行统计,整理见下表:
解答下列问题:
(1)在这个问题中,总体是______,样本容量a=______;
(2)第四小组的频率c=______;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
| 组别 | 分组 | 频数 | 频率 |
| 1 | 49.5~59.5 | 60 | 0.12 |
| 2 | 59.5~69.5 | 120 | 0.24 |
| 3 | 69.5~79.5 | 180 | 0.36 |
| 4 | 79.5~89.5 | 130 | c |
| 5 | 89.5~99.5 | b | 0.02 |
| 合计 | a | 1.00 | |
(1)在这个问题中,总体是______,样本容量a=______;
(2)第四小组的频率c=______;
(3)被抽取的学生成绩的中位数落在第几小组内?
(4)若成绩在90分以上(含90分)的学生获一等奖,请你估计全市获一等奖的人数.
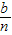 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.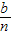 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.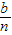 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.