题目内容
【题目】△ABC中,AC=BC,∠ACB=90°,点D在AB上,E在BC上,且AD=BE,BD=AC.
(1)如图1,求证:DC=DE;
(2)如图2,过E作EF⊥AB于F,若BF=2,求CE的长.
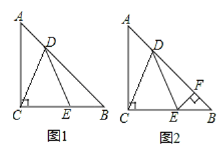
【答案】(1)见解析;(2)4
【解析】
(1)根据SAS证明△ACD≌△BDE,再根据全等三角形的性质即可得DC=DE, 即为所求;
(2)过D作DG⊥CE于G, 过E作EF⊥AB于F,根据等腰直角三角形的性质求出EF的长,根据题意求出∠EDG=∠EDF,根据角平分线的性质求出EG=EF,根据等腰三角形的性质得到答案.
(1)证明:∵AC=BC,∠ACB=90°
∴∠A=∠B=45°
在△ACD和△BDE中

∴△ACD≌△BDE(SAS)
∴DC=DE
(2)解:∵△ACD≌△BDE
∴∠ACD=∠BDE
∵AC=BC,∠B=45°
∴∠BCD=∠BDC=67.5°
∴∠ACD=∠BDE=22.5°
∠CDE=45°
过D作DG⊥CE于G
∵DC=DE
∴∠CDG=∠EDG=22.5°,CG=EG
∴∠CDG=∠EDG=∠EDF =22.5°
∵DG⊥BC,EF⊥AB,∠B=45°
∴FE=EG=GC=FB=2
∴CE=2FB=4


练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目




