题目内容
如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上,点D落在D′处,C′D′交AE于点M.若AB=6,BC=9,则AM的长为 .


解:根据折叠的性质可知,FC=FC′,∠C=∠FC′M=90°,
设BF=x,则FC=FC′=9﹣x,
∵BF2+BC′2=FC′2,
∴x2+32=(9﹣x)2,
解得:x=4,
∵∠FC′M=90°,
∴∠AC′M+∠BC′F=90°,
又∵∠BFC′+BC′F=90°,
∴∠AC′M=∠BFC′
∵∠A=∠B=90°
∴△AMC′∽△BC′F
∴
∵BC′=AC′=3,
∴AM= .
.
故答案为: .
.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为( )
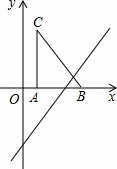
|
| A.] | 4 | B. | 8 | C. | 16 | D. | 8 |
若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个交点,坐标分别为(x1,0)、(x2,0),且x1<x2,图象上有一点M(x0,y0),在x轴下方,则下列判断正确的是( )
|
| A. | a(x0﹣x1)(x0﹣x2)<0 | B. | a>0 |
|
| C. | b2﹣4ac≥0 | D. | x1<x0<x2 |
将连续正整数按如下规律排列:
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 1 | 2 | 3 | 4 | |
| 第2行 | 8 | 7 | 6 | 5 | |
| 第3行 | 9 | 10 | 11 | 12 | |
| 第4行 | 16 | 15 | 14 | 13 | |
| 第5行 | 17 | 18 | 19 | 20 | |
| ……… |
若正整数565位于第 行,第
行,第 列,则
列,则 = 。
= 。
在数轴上表示﹣2的点与表示3的点之间的距离是( )
|
| A. | 5 | B. | ﹣5 | C. | 1 | D. | ﹣1 |
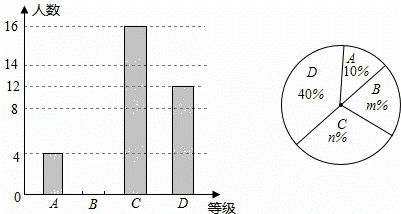
 (2)求这50名同学捐款的平均数
(2)求这50名同学捐款的平均数






 B、
B、 C、2 D、-2
C、2 D、-2