题目内容
如图，已知AB=6，BC=4，D为AC的中点，求线段BD的长．
解：∵AB=6，BC=4，
∴AC=6-4=2，
∵D为AC的中点，
∴DC=
AC=1，
∴BD=CD+BC=1+4=5．
分析：先计算出AC=2，再根据线段中点的定义得到DC=1，然后利用CD+BC即可．
点评：本题考查了两点间的距离：连接两点间的线段的长度叫两点间的距离．
∴AC=6-4=2，
∵D为AC的中点，
∴DC=
AC=1，∴BD=CD+BC=1+4=5．
分析：先计算出AC=2，再根据线段中点的定义得到DC=1，然后利用CD+BC即可．
点评：本题考查了两点间的距离：连接两点间的线段的长度叫两点间的距离．
练习册系列答案
相关题目
24、如图，已知AB=AC，∠1=∠2，∠3=∠F，试判断EC与DF是否平行，并说明理由．
17、（保留作图痕迹）如图，已知AB=DC．
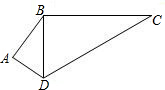如图，已知AB=4，BC=12，CD=13，DA=3，AB⊥AD．判断BC⊥BD吗？简述你的理由．
如图：已知AB∥DE，点C是AE的中点，
如图，已知AB、CD交于点O，且点O是AB的中点，AC∥BD，请说明点O是CD的中点的理由．