Question

类比梯形的定义，我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．

（1）已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A＝70°，∠B＝80°．求∠C，∠D的度数．

（2）在探究“等对角四边形”性质时：

①小红画了一个“等对角四边形”ABCD（如图2），其中∠ABC＝∠ADC，AB＝AD，此时她发现CB＝CD成立．请你证明此结论；

②由此小红猜想：“对于任意‘等对角四边形’，当一组邻边相等时，另一组邻边也相等”．你认为她的猜想正确吗?若正确，请证明；若不正确，请举出反例．

（3）已知：在“等对角四边形"ABCD中，∠DAB＝60°，∠ABC=90°，AB＝5，AD＝4．求对角线AC的长．

 

 

Answer 1

（1）130°，80°；（2）①证明见解析；②不正确，反例见解析；（3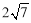）或．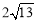

【解析】

试题分析：（1）根据定义和四边形内角和定理求解即可．

（2）①连接BD，根据定义以及等腰三角形的判定和性质求证即可．

②当相等角的两边相等时，结论不正确．

（3）分∠ADC＝∠ABC＝90°和∠BCD＝∠DAB＝60°两种情况讨论即可．

试题解析：（1）∵等对角四边形ABCD中，∠A≠∠C，∠B＝80°，∴∠Ｄ＝∠B＝80°．

∵∠A＝70°，∴．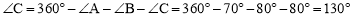

（2）①如图，连接BD，

∵AB＝AD，∴．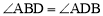

∵，∴．

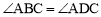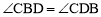∴CB＝CD．

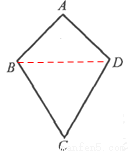
②不正确，反例如图，∠A＝∠C＝90°，AB＝AD，但CB≠CD．

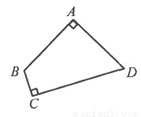
（3）①如图，当∠ADC＝∠ABC＝90°时，延长AD,BC交于点F，

∵∠ABC＝90°，∠DAB＝60°，AB=5，∴AE=10．

∴．

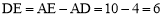∵∠EDC＝90°，∠E＝30°，∴．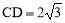

∴．

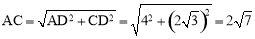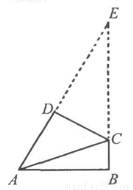
②如图，当∠BCD＝∠DAB＝60°时，过D点作DE⊥AB于点E，DF⊥BC于点F，

∵DE⊥AB，∠DAB＝60°，AD＝4，∴．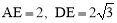

∴．

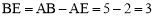∵四边形BFDE是矩形，∵．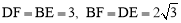

∵∠BCD＝60°，∴．∴．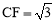

∴

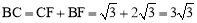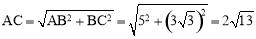
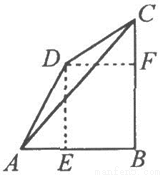
考点：1．新定义和阅读理解型问题；2．四边形内角和定理；3．等腰三角形的判定和性质；4．勾股定理；5．含30度角直角性质；6．分类思想和反证法的应用．