Question

【题目】P是△ABC内一点，∠PBC＝30°，∠PBA＝8°，且∠PAB＝∠PAC＝22°，则∠APC的度数为_____．

Answer 1

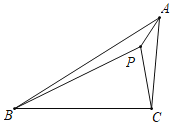
【答案】142°

【解析】

在AC的延长线上截取AF=AB，连BF，PF，延长AP交BC于D，交BF于E，证得△APB≌△APF，则AP为BF的垂直平分线，由∠PBA=8°可得∠CBF=30°=∠CBP，∠BFP=60°=∠BPF，可得BC平分PF，进一步可求出∠APC的度数．

在AC的延长线上截取AF＝AB，连BF，PF，延长AP交BC于D，交BF于E，

在△APB和△APF中，

，

∴△APB≌△APF（SAS），

∴AB＝AF，PB＝PF，∠AFP＝∠ABP＝8°，

∴AP垂直平分BF，∠BPE＝∠BAP+∠ABP＝30°°，∠FPE＝∠CAP+∠AFP＝30°

∴∠AEP=∠FEP=90°，

∴∠PBF=∠PFB=60°

∵∠PBC＝30°

∴∠CBF＝30°＝∠PBC，∠BPF＝∠BFP＝∠PBF=60°，

∴三角形BPF是等边三角形，BC平分∠PBF

∴BC垂直平分PF

∴PC=PF

∴∠CPF＝∠CFP＝8°

∴∠DPC＝38°

∴∠APC＝142°；

故答案为：142°．