题目内容
(1)计算:(2 -3
-3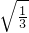 )×
)×
(2)用配方法解方程:x2-2x-5=0.
解:(1)原式=(4 -
- )×
)×
=3 ×
×
=9 ;
;
(2)x2-2x=5,
∴x2-2x+1=6,
∴(x-1)2=6,
∴x-1=± ,
,
∴x1=1+ ,x2=1-
,x2=1- .
.
分析:(1)先把括号内的二次根式化为最简二次根式,然后后进行乘法运算即可;
(2)先把常数项移到方程右边得到x2-2x=5,再把方程两边都加上1,则方程左边可配成完全平方式,然后利用直接开平方法求解.
点评:本题考查了解一元二次方程-配方法:先把一元二次方程的二次项的系数化为1和常数项移到方程右边,再方把方程两边加上一次项系数的一半,这样方程左边配成了完全平方式,然后利用直接开平方法解方程.也考查了二次根式的混合运算.
 -
- )×
)×
=3
 ×
×
=9
 ;
;(2)x2-2x=5,
∴x2-2x+1=6,
∴(x-1)2=6,
∴x-1=±
 ,
,∴x1=1+
 ,x2=1-
,x2=1- .
.分析:(1)先把括号内的二次根式化为最简二次根式,然后后进行乘法运算即可;
(2)先把常数项移到方程右边得到x2-2x=5,再把方程两边都加上1,则方程左边可配成完全平方式,然后利用直接开平方法求解.
点评:本题考查了解一元二次方程-配方法:先把一元二次方程的二次项的系数化为1和常数项移到方程右边,再方把方程两边加上一次项系数的一半,这样方程左边配成了完全平方式,然后利用直接开平方法解方程.也考查了二次根式的混合运算.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
