题目内容
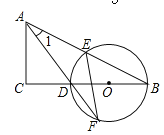
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,
交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.

(1)求证:直线DF与⊙O相切;
(2)若AE=7,BC=6,求AC的长.
【答案】![]() 证明见解析;
证明见解析;![]()
![]()
【解析】
试题分析:![]() 首先连接OD,根据等腰三角形的性质可证∠C=∠ODC,从而可证∠B=∠ODC,根据DF⊥AB可证DF⊥OD,所以可证线DF与⊙O相切;
首先连接OD,根据等腰三角形的性质可证∠C=∠ODC,从而可证∠B=∠ODC,根据DF⊥AB可证DF⊥OD,所以可证线DF与⊙O相切;
![]() 根据圆内接四边形的性质可得:△BCA∽△BED,所以可证:
根据圆内接四边形的性质可得:△BCA∽△BED,所以可证:![]() ,解方程求出BE的长度,从而求出AC的长度.
,解方程求出BE的长度,从而求出AC的长度.
试题解析:![]() 如图所示,
如图所示,
连接![]() ,
,

∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ∥
∥![]() ,
,
∵![]() ,
,
∴![]() ;
;
∵点![]() 在⊙O上,
在⊙O上,
∴直线![]() 与⊙O相切;
与⊙O相切;
![]() ∵四边形
∵四边形![]() 是⊙O的内接四边形,
是⊙O的内接四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴△BED∽△BCA,
∴![]() ,
,
∵OD∥AB,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目