题目内容
如图，有一圆柱体高为20cm，底面半径为5cm，在圆柱的下底面A点处有一蜘蛛，它想吃到上底面上与A相对的B点处的苍蝇，需爬行的最短路径约是25
25
cm．（圆周率的值取3）分析：要求需要爬行的最短路径首先要把圆柱的侧面积展开，得到一个矩形，然后利用勾股定理求两点间的线段即可．
解答：
解：如图所示，把圆柱得侧面展开，得到如图所示的图形，
其中AC=πR=5π=5×3=15cm，BC=20cm，
在Rt△ABC中，AB=
=
=25cm，
所以需爬行的最短路径约是25cm，
故答案为：25．
解：如图所示，把圆柱得侧面展开，得到如图所示的图形，其中AC=πR=5π=5×3=15cm，BC=20cm，
在Rt△ABC中，AB=
| AC2+BC2 |
| 625 |
所以需爬行的最短路径约是25cm，
故答案为：25．
点评：本题考查了平面展开-最短路径问题，解题的关键是理解要求需要爬行的最短路径首先要把圆柱的侧面积展开，底面周长和高以及所走的路线构成一个直角三角形，然后再求线段的长．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
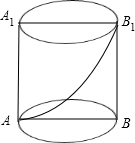如图：有一圆柱体高为8πcm，底面圆的半径为6cm，AA1、BB1为相对的两条母线，在点A处有一个蜘蛛，点B处有一只苍蝇，蜘蛛沿圆柱体侧面爬到B1处吃掉苍蝇，问蜘蛛所爬过的最短路径长是多少？
如图：有一圆柱体高为8πcm，底面圆的半径为6cm，AA1、BB1为相对的两条母线，在点A处有一个蜘蛛，点B处有一只苍蝇，蜘蛛沿圆柱体侧面爬到B1处吃掉苍蝇，问蜘蛛所爬过的最短路径长是多少？
和根号的式子表示）