题目内容
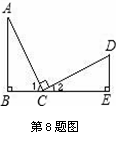
 已知:如图所示,AC⊥CD,BD⊥CD.线段AB的垂直平分线EF交AB于点E,交CD于点F,且AC=FD,求证:△ABF是等腰直角三角形.
已知:如图所示,AC⊥CD,BD⊥CD.线段AB的垂直平分线EF交AB于点E,交CD于点F,且AC=FD,求证:△ABF是等腰直角三角形.
证明:∵EF是AB的垂直平分线,
∴FA=FB.
∵AC⊥CD,BD⊥CD,
∴△ACF与△FDB是直角三角形.
在Rt△ACF与Rt△FDB中,AC=FD,FA=BF,
∴Rt△ACF≌Rt△FDB(HL).
∴∠CAF=∠DFB.
∵∠C=90°,
∴∠CAF+∠CFA=90°,
∴∠CFA+∠BFD=90°,
∴∠AFB=90°.
∴△ABF是等腰直角三角形.
分析:根据线段垂直平分线的性质,得FA=FB,只需证明∠AFB=90°.根据HL可以证明Rt△ACF≌Rt△FDB,则∠CAF=∠DFB,结合∠CAF+∠CFA=90°,即可求证.
点评:此题综合运用了线段垂直平分线的性质、全等三角形的判定和性质.
∴FA=FB.
∵AC⊥CD,BD⊥CD,
∴△ACF与△FDB是直角三角形.
在Rt△ACF与Rt△FDB中,AC=FD,FA=BF,
∴Rt△ACF≌Rt△FDB(HL).
∴∠CAF=∠DFB.
∵∠C=90°,
∴∠CAF+∠CFA=90°,
∴∠CFA+∠BFD=90°,
∴∠AFB=90°.
∴△ABF是等腰直角三角形.
分析:根据线段垂直平分线的性质,得FA=FB,只需证明∠AFB=90°.根据HL可以证明Rt△ACF≌Rt△FDB,则∠CAF=∠DFB,结合∠CAF+∠CFA=90°,即可求证.
点评:此题综合运用了线段垂直平分线的性质、全等三角形的判定和性质.

练习册系列答案
相关题目
 25、已知:如图所示,AC,BD相交于点O,BE,CE分别平分∠ABD,∠ACD,∠A=50°,∠D=44°,求∠E的度数.
25、已知:如图所示,AC,BD相交于点O,BE,CE分别平分∠ABD,∠ACD,∠A=50°,∠D=44°,求∠E的度数. 19、已知:如图所示BF⊥AC,AD⊥BC,且相交于点E,BD=AD,连接CE.说明△DCE是等腰三角形的理由.
19、已知:如图所示BF⊥AC,AD⊥BC,且相交于点E,BD=AD,连接CE.说明△DCE是等腰三角形的理由. 26、已知:如图所示,AC⊥CD,BD⊥CD.线段AB的垂直平分线EF交AB于点E,交CD于点F,且AC=FD,求证:△ABF是等腰直角三角形.
26、已知:如图所示,AC⊥CD,BD⊥CD.线段AB的垂直平分线EF交AB于点E,交CD于点F,且AC=FD,求证:△ABF是等腰直角三角形.