题目内容
如图,⊙O1和⊙O2内切于点A,⊙O2的弦BC经过⊙O1上一点D,AB、AC分别交⊙O1于E、F,A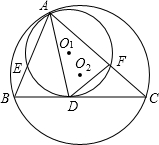 D平分∠BAC.
D平分∠BAC.(1)求证:BC是⊙O1的切线;
(2)若⊙O1与⊙O2的半径之比等于2:3,BD=2
| 3 |
| 10 |
分析:(1)过点A作两圆外切线PQ,作⊙O1的直径DK,连接KF,EF,首先证明由∠EFA=∠C证明EF∥BC,最终可证明∠FDC+∠KDF=90°;
(2)连接O1O2,则直线O1O2必过A点,作O1M⊥AB,O2N⊥AB,M,N为垂足,首先证明AE、BE、AB的等量关系,根据切线定理,即可算出BE、AB,最后计算出AD.
(2)连接O1O2,则直线O1O2必过A点,作O1M⊥AB,O2N⊥AB,M,N为垂足,首先证明AE、BE、AB的等量关系,根据切线定理,即可算出BE、AB,最后计算出AD.
解答: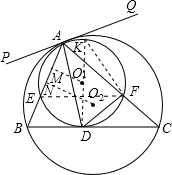 (1)证明:过点A作两圆外切线PQ,作⊙O1的直径DK,连接KF,EF,
(1)证明:过点A作两圆外切线PQ,作⊙O1的直径DK,连接KF,EF,
则∠EFA=∠PAB,∠C=∠PAB.
∴∠EFA=∠C.
∴EF∥BC.
∵AD平分∠BAC,∴∠BAD=∠CAD,
∴∠FDC=∠EFD=∠BAD=∠CAD=∠DKF.
∵DK是⊙O1的直径,∴∠KDF+∠DKF=90°,∠FDC+∠KDF=90°.
∴DO1⊥DC.
∴BC是⊙O1的切线.
(2)解:连接O1O2,则直线O1O2必过A点,
作O1M⊥AB,O2N⊥AB,M,N为垂足,则O1M∥O2N,
且AM=
AE•AN=
AB,
∴
=
=
=
.
∴AE=2BE,AB=3BE.
∵BC切圆O1于D,∴BD2=BE•BA=3BE2
∴BE2=4.
∵BE>0,∴BE=2,∴AB=3BE=6
∵BD为⊙O2的切线,∴∠ADB=∠AFD,
∴
=
=
=
,
∴AD=
.
 (1)证明:过点A作两圆外切线PQ,作⊙O1的直径DK,连接KF,EF,
(1)证明:过点A作两圆外切线PQ,作⊙O1的直径DK,连接KF,EF,则∠EFA=∠PAB,∠C=∠PAB.
∴∠EFA=∠C.
∴EF∥BC.
∵AD平分∠BAC,∴∠BAD=∠CAD,
∴∠FDC=∠EFD=∠BAD=∠CAD=∠DKF.
∵DK是⊙O1的直径,∴∠KDF+∠DKF=90°,∠FDC+∠KDF=90°.
∴DO1⊥DC.
∴BC是⊙O1的切线.
(2)解:连接O1O2,则直线O1O2必过A点,
作O1M⊥AB,O2N⊥AB,M,N为垂足,则O1M∥O2N,
且AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AE |
| AB |
| AM |
| AN |
| AO1 |
| AO2 |
| 2 |
| 3 |
∴AE=2BE,AB=3BE.
∵BC切圆O1于D,∴BD2=BE•BA=3BE2
∴BE2=4.
∵BE>0,∴BE=2,∴AB=3BE=6
∵BD为⊙O2的切线,∴∠ADB=∠AFD,
∴
| AB |
| AD |
| BD |
| DF |
| 6 |
| AD |
2
| ||
|
∴AD=
| 30 |
点评:本题考查了切线的判定,平行线分线段成比例等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
 20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明.
20、已知:如图,⊙O1和⊙O2相交于A、B两点,动点P在⊙O2上,且在⊙1外,直线PA、PB分别交⊙O1于C、D,问:⊙O1的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明. 长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点.
长⊙O1相交于C点,连接BC,过A点作AE∥BC与⊙O相交于E点,与BD相交于F点.
 、PB的延长线分别交⊙O2于点E、F,PB交AC于D.
、PB的延长线分别交⊙O2于点E、F,PB交AC于D. 16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC.
16、如图.⊙O1和⊙O2外切于点A,BC是⊙O1和⊙O2的公切线,B、C为切点,求证:AB⊥AC. (2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.
(2001•黄冈)已知,如图,⊙O1和⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.