Question

【题目】请完成以下问题：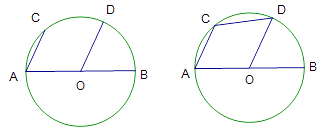

图1 图2
（1）如图1， ，弦 与半径 平行，求证： 是⊙ 的直径；
（2）如图2， 是⊙ 的直径，弦 与半径 平行.已知圆的半径为 ， ， ，求 与 的函数关系式.

Answer 1

【答案】
（1）证明：连结 ，交 于点

∵
∴OD⊥BC，即
又AC∥OD，

弦 是圆的直径（ 的圆周角所对的弦是直径）
（2）解：如图，连结 ，连结 交 于点

是⊙ 的直径

弦 与半径 平行



，
得
是 的中点
是 的中位线


即
化简得：
【解析】（1）连结 B C ，交 O D 于点 H，通过证明∠ACB=∠OHB=90°，根据圆周角定理可得弦 A B 是圆的直径；（2）连结 A D , B D ，连结 B C 交 O D 于点 H，根据已知条件可证DBH~DAB，得出成比例的线段，从而问题得解。