题目内容
【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2![]() ;
;
④四边形ACEB的面积是16.
则以上结论正确的是( )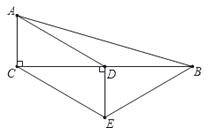
A.①②③
B.①②④
C.①③④
D.②④
【答案】A
【解析】解:①∵∠ACB=90°,DE⊥BC,
∴∠ACD=∠CDE=90°,
∴AC∥DE,
∵CE∥AD,
∴四边形ACED是平行四边形,故①正确;
②∵D是BC的中点,DE⊥BC,
∴EC=EB,
∴△BCE是等腰三角形,故②正确;
③∵AC=2,∠ADC=30°,
∴AD=4,CD=2![]() ,
,
∵四边形ACED是平行四边形,
∴CE=AD=4,
∵CE=EB,
∴EB=4,DB=2![]() ,
,
∴CB=4![]() ,
,
∴AB=![]() =2
=2![]() ,
,
∴四边形ACEB的周长是10+2![]() 故③正确;
故③正确;
④四边形ACEB的面积:![]() ×2×4
×2×4![]() +
+![]() ×4
×4![]() ×2=8
×2=8![]() , 故④错误,
, 故④错误,
故选:A.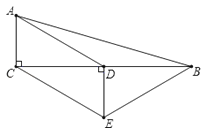
证明AC∥DE,再由条件CE∥AD可证明四边形ACED是平行四边形;根据线段的垂直平分线证明AE=EB可得△BCE是等腰三角形;首先利用三角函数计算出AD=4,CD=2![]() , 再算出AB长可得四边形ACEB的周长是10+2
, 再算出AB长可得四边形ACEB的周长是10+2![]() , 利用△ACB和△CBE的面积和可得四边形ACEB的面积.
, 利用△ACB和△CBE的面积和可得四边形ACEB的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






