题目内容
 如图,是一块四边形稻田ABCD,∠B=90°,AB=9cm,BC=12cm,CD=AD=15m,根据这些数据计算这块稻田的面积(精确到1m2)
如图,是一块四边形稻田ABCD,∠B=90°,AB=9cm,BC=12cm,CD=AD=15m,根据这些数据计算这块稻田的面积(精确到1m2)考点:勾股定理,等边三角形的判定与性质
专题:
分析:连接AC,过点C作CE⊥AD于点E,先根据勾股定理求出AC的长,判断出△ACD的形状,再求出CE的长,根据S四边形ABCD=S△ABC+S△ACD即可得出结论.
解答: 解:连接AC,过点C作CE⊥AD于点E,
解:连接AC,过点C作CE⊥AD于点E,
∵∠B=90°,AB=9m,BC=12m,
∴AC=
=
=15m.
∵CD=AD=15m,
∴△ACD是等边三角形,
∴CE=CD•sin60°=15×
=
,
∴S四边形ABCD=S△ABC+S△ACD=
×9×12+
×15×
=54+
≈54+96=150(m2).
答:这块稻田的面积是150平方米.
 解:连接AC,过点C作CE⊥AD于点E,
解:连接AC,过点C作CE⊥AD于点E,∵∠B=90°,AB=9m,BC=12m,
∴AC=
| AB2+BC2 |
| 92+122 |
∵CD=AD=15m,
∴△ACD是等边三角形,
∴CE=CD•sin60°=15×
| ||
| 2 |
15
| ||
| 2 |
∴S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
15
| ||
| 2 |
225
| ||
| 4 |
答:这块稻田的面积是150平方米.
点评:本题考查的是勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
有理数-0.3,-
,-
之间的大小关系正确的是( )
| 1 |
| 3 |
| 1 |
| 4 |
A、-
| ||||
B、-
| ||||
C、-0.3<-
| ||||
D、-
|
方程x2-x-1=0的两个实根是m、n,则代数式(m2-m+2014)(m+n)的值为( )
| A、2014 | B、0 |
| C、2015 | D、-1 |
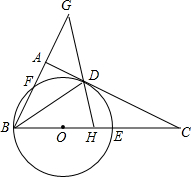 如图,BD为Rt△ABC的角平分线,以BC边上一点O为圆心,过点B、D两点作⊙O,⊙O分别交BC、AB于E、F两点.
如图,BD为Rt△ABC的角平分线,以BC边上一点O为圆心,过点B、D两点作⊙O,⊙O分别交BC、AB于E、F两点.