题目内容
如果a-b=2,a-c=
,那么a2+b2+c2-ab-ac-bc等于( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
分析:把多项式扩大二倍,根据完全平方公式写成三个完全平方式,然后根据a-b=2,a-c=
,求出b-c,代入求解即可.
| 1 |
| 2 |
解答:解:a2+b2+c2-ab-ac-bc,
=
(2a2+2b2+2c2-2ab-2ac-2bc),
=
[(a2+b2-2ab)+(a2+c2-2ac)+(b2+c2-2bc)],
=
[(a-b)2+(a-c)2+(b-c)2],
∵a-b=2,a-c=
,
∴b-c=-
,
∴原式=
(4+
+
)=
.
故选A.
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∵a-b=2,a-c=
| 1 |
| 2 |
∴b-c=-
| 3 |
| 2 |
∴原式=
| 1 |
| 2 |
| 1 |
| 4 |
| 9 |
| 4 |
| 13 |
| 4 |
故选A.
点评:本题是完全平方公式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式,解题关键是对原多项式扩大二倍凑成完全平方式.

练习册系列答案
相关题目
如果关于x的不等式组
无解,则m的取值范围是( )
|
| A、m>3 | B、m≥3 |
| C、m<3 | D、m≤3 |
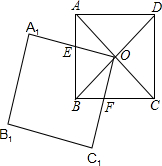 于点E,OC1交BC于点F.
于点E,OC1交BC于点F. ,请问小军至少几次进入迷宫中心?
,请问小军至少几次进入迷宫中心?