题目内容
 如图,∠AOB=100°,OF是∠BOC的平分线,∠AOE=∠EOD,∠EOF=140°,求:∠COD的度数.
如图,∠AOB=100°,OF是∠BOC的平分线,∠AOE=∠EOD,∠EOF=140°,求:∠COD的度数.
分析:设∠COD=x,∠BOC+∠AOD=y,由OF平分∠BOC,∠AOE=∠DOE,可得x+
y=140°,图中六个角之和为360°,可得x+y+100°=360°,联立方程组解得x.
| 1 |
| 2 |
解答:解:设∠COD=x,∠BOC+∠AOD=y,
∵OF平分∠BOC,∠AOE=∠DOE,
∴x+
y=140°①,
∵六个角之和为360°,
∴x+y+100°=360°②,
联立①②解得:x=20°,
∴∠COD的度数为20°.
故答案为:20°.
∵OF平分∠BOC,∠AOE=∠DOE,
∴x+
| 1 |
| 2 |
∵六个角之和为360°,
∴x+y+100°=360°②,
联立①②解得:x=20°,
∴∠COD的度数为20°.
故答案为:20°.
点评:本题考查角与角之间的运算,注意结合图形,发现角与角之间的关系,进而求解,难度适中.

练习册系列答案
相关题目
 如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11,的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,…,观察图中的规律,求出第10个黑色梯形的面积S10=
如图,∠AOB=45°,过OA上到点O的距离分别为1,3,5,7,9,11,的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3,S4,…,观察图中的规律,求出第10个黑色梯形的面积S10=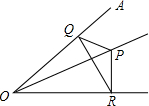 如图,∠AOB=45°,角内有点P,PO=10,在角的两边上有两点Q,R(均不同于O点),则△PQR的周长的最小值为
如图,∠AOB=45°,角内有点P,PO=10,在角的两边上有两点Q,R(均不同于O点),则△PQR的周长的最小值为 3、如图,∠AOB=90°,其中锐角的个数共有( )
3、如图,∠AOB=90°,其中锐角的个数共有( ) 如图,△AOB中,OA=OB=10,∠AOB=120°,以O为圆心,5为半径的⊙O与OA、OB相交.
如图,△AOB中,OA=OB=10,∠AOB=120°,以O为圆心,5为半径的⊙O与OA、OB相交. 如图,∠AOB是一角度为10°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF、FG、GH…,且OE=EF=FG=GH…,在OA、OB足够长的情况下,最多能添加这样的钢管的根数为( )
如图,∠AOB是一角度为10°的钢架,要使钢架更加牢固,需在其内部添加一些钢管:EF、FG、GH…,且OE=EF=FG=GH…,在OA、OB足够长的情况下,最多能添加这样的钢管的根数为( )