题目内容

如图，点A和点B在第一象限，A是反比例函数y= $数学公式$ 上的一点，B是反比例函数y= $数学公式$ 上的一点，且AB平行于x轴，连接OA、OB，则△AOB的面积为________．

1
分析：设点A的纵坐标为b，根据反比例函数的解析式求出点A、B的横坐标，然后求出AB的长，再根据三角形的面积公式列式计算即可得解．
解答：设点A的纵坐标为b，
所以， $\text{[math]}$ =b，
解得x= $\text{[math]}$
∵AB平行于x轴，
∴点B的横坐标为b，
∴ $\text{[math]}$ =b，
x= $\text{[math]}$ ，
∴AB= $\text{[math]}$ - $\text{[math]}$ = $\text{[math]}$ ，
∴△AOB的面积= $\text{[math]}$ × $\text{[math]}$ •b=1．
故答案为：1．
点评：本题考查了反比例函数系数的几何意义，用点A的纵坐标表示出AB的长度是解题的关键．

练习册系列答案

寒假集训合肥工业大学出版社系列答案

寒假作业沈阳出版社系列答案

快乐天天练假期作业寒安徽师范大学出版社系列答案

寒假作业河北少年儿童出版社系列答案

赢在寒假安徽人民出版社系列答案

活力假期暑假系列答案

快乐寒假武汉出版社系列答案

走进寒假假期快乐练电子科技大学出版社系列答案

学习报快乐寒假系列答案

寒假作业广州出版社系列答案

相关题目

27、如图，直线AC∥BD，连接AB，直线AC，BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA，PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）
（1）当动点P落在第①部分时，求证：∠APB=∠PAC+∠PBD；
（2）当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（直接回答成立或不成立）
（3）当动点P在第③部分时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以证明．

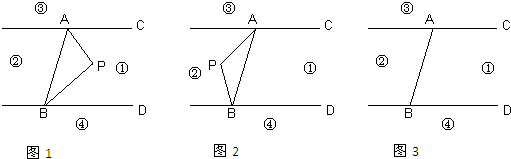
（2012•房山区一模）已知：如图，点P是线段AB上的动点，分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD，AD和BC交于点M．
（1）当△APC和△BPD面积之和最小时，直接写出AP：PB的值和∠AMC的度数；
（2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α，当α＜60°时，旋转过程中，∠AMC的度数是否发生变化？证明你的结论．
（3）在第（2）小题给出的旋转过程中，若限定60°＜α＜120°，∠AMC的大小是否会发生变化？若变化，请写出∠AMC的度数变化范围；若不变化，请写出∠AMC的度数．

如图，直线AC∥BD，连接AB，直线AC，BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分．当动点P落在某个部分时，连接PA，PB，构成∠PAC，∠APB，∠PBD三个角．（提示：有公共端点的两条重合的射线所组成的角是0°角）
（1）当动点P落在第①部分时，试说明∠APB=∠PAC+∠PBD；
（2）当动点P落在第②部分时，∠APB=∠PAC+∠PBD是否成立？（直接回答成立或不成立）
（3）当动点P在第③部分时，全面探究∠PAC，∠APB，∠PBD之间的关系，并写出动点P的具体位置和相应的结论．选择其中一种结论加以说明．

已知：如图，点P是线段AB上的动点，分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD，AD和BC交于点M．
（1）当△APC和△BPD面积之和最小时，直接写出AP：PB的值和∠AMC的度数；
（2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α，当α＜60°时，旋转过程中，∠AMC的度数是否发生变化？证明你的结论．
（3）在第（2）小题给出的旋转过程中，若限定60°＜α＜120°，∠AMC的大小是否会发生变化？若变化，请写出∠AMC的度数变化范围；若不变化，请写出∠AMC的度数．

已知：如图，点P是线段AB上的动点，分别以AP、BP为边向线段AB的同侧作正△APC和正△BPD，AD和BC交于点M．
（1）当△APC和△BPD面积之和最小时，直接写出AP：PB的值和∠AMC的度数；
（2）将点P在线段AB上随意固定，再把△BPD按顺时针方向绕点P旋转一个角度α，当α＜60°时，旋转过程中，∠AMC的度数是否发生变化？证明你的结论．
（3）在第（2）小题给出的旋转过程中，若限定60°＜α＜120°，∠AMC的大小是否会发生变化？若变化，请写出∠AMC的度数变化范围；若不变化，请写出∠AMC的度数．