题目内容

如图，O为矩形ABCD的中心，将直角三角板的直角顶点与O点重合，转动三角板使两直角边始终与BC，AB相交，交点分别为M，N，如果AB=4，AD=6，OM=x，ON=y，则y与x的关系是______．
精英家教网
作OP垂直AB于点P，OQ垂直BC于点Q．
精英家教网

∵∠PON+∠POM=90°，∠POM+∠MOQ=90°
∴∠PON=∠MOQ，
又∵∠NPO=∠MQO，
∴△ONP∽△OMQ，
OP：OQ=
1
2
AD：
1
2
AB=ON：OM．
所以y=
3
2
x．
故答案为y=
3
2
x
练习册系列答案
相关题目
26、如图，在等边△ABC中，点D是BC边的中点，以AD为边作等边△ADE．
（1）求∠CAE的度数；
（2）取AB边的中点F，连接CF、CE，试证明四边形AFCE是矩形．
如图，等边三角形ABC，边长为2，AD是BC边上的高．
（1）在△ABC内部作一个矩形EFGH（如图1），其中E、H分别在边AB、AC上，FG在边BC上．
①设矩形的一边FG=x，那么EF=
 
．（用含有x的代数式表示）
②设矩形的面积为y，当x取何值时，y的值最大，最大值是多少？
（2）在图2中，只用圆规画出点E，使得上述矩形EFGH面积最大．写出画法，并保留作图痕迹．
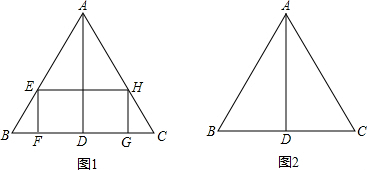
精英家教网
定义：只有一组对角是直角的四边形叫做损矩形，连接它的两个非直角顶点的线段叫做这个损矩形的直径．
（1）如图1，损矩形ABCD，∠ABC=∠ADC=90°，则该损矩形的直径是线段
 
．
（2）在线段AC上确定一点P，使损矩形的四个顶点都在以P为圆心的同一圆上（即损矩形的四个顶点在同一个圆上），请作出这个圆，并说明你的理由．友情提醒：“尺规作图”不要求写作法，但要保留作图痕迹．
（3）如图2，△ABC中，∠ABC=90°，以AC为一边向形外作菱形ACEF，D为菱形ACEF的中心，连接BD，当BD平分∠ABC时，判断四边形ACEF为何种特殊的四边形？请说明理由．若此时AB=3，BD=4
2
，求BC的长．
精英家教网精英家教网
如图，四边形DEFG是△ABC的内接矩形，如果△ABC的高线AH长8cm，底边BC长10cm，设DG=xcm，DE=ycm，则y关于x的函数关系式为
y=-
4
5
x+8
y=-
4
5
x+8
．
（1）如图1，在平行四边形ABCD中，E、F为BC上两点，且BE=CF，AF=DE．
求证：①△ABF≌△DCE；②四边形ABCD是矩形．
（2）如图2，已知△ABC是等边三角形，D点是AC的中点，延长BC到E，使CE=CD．
①请用尺规作图的方法，过点D作DM⊥BE，垂足为M；（不写作法，保留作图痕迹）
②求证：BM=EM．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网