题目内容
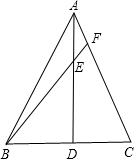 如图,已知等腰△ABC的面积是21,且AD⊥BC,AE:ED=1:3,BE的延长线交AC于F,则S△ABF=________.
如图,已知等腰△ABC的面积是21,且AD⊥BC,AE:ED=1:3,BE的延长线交AC于F,则S△ABF=________.
3
分析:首先过点E作EK∥CD交AC于K,根据平行线分线段成比例定理,即可得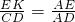 =
=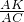 ,
,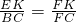 ,又由AE:ED=1:3,可得
,又由AE:ED=1:3,可得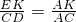 =
= ,然后根据等腰三角形的性质,求得FK:FC=1:8,设FK=x,求得AF:AC的值,即可求得S△ABF的值.
,然后根据等腰三角形的性质,求得FK:FC=1:8,设FK=x,求得AF:AC的值,即可求得S△ABF的值.
解答: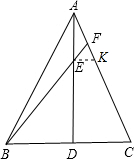 解:过点E作EK∥CD交AC于K,
解:过点E作EK∥CD交AC于K,
∴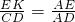 =
=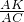 ,
,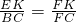 ,
,
∵AE:ED=1:3,
∴AE:AD=1:4,
∴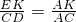 =
= ,
,
∵AB=AC,AD⊥BC,
∴BC=2CD,
∴EK:BC=1:8,
∴FK:FC=1:8,
设FK=x,则CK=7x,
∴AK= x,
x,
∴AC=AK+CK= x,
x,
∴AF=AK-FK= x-x=
x-x= x,
x,
∴AF:AC=1:7,
∵S△ABC=21,
∴S△ABF= S△ABC=3.
S△ABC=3.
故答案为:3.
点评:此题考查了平行线分线段成比例定理、等腰三角形的性质以及等高三角形面积的关系.此题难度较大,解题的关键是准确作出辅助线,利用数形结合思想与方程思想求解.
分析:首先过点E作EK∥CD交AC于K,根据平行线分线段成比例定理,即可得
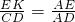 =
=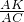 ,
,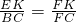 ,又由AE:ED=1:3,可得
,又由AE:ED=1:3,可得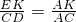 =
= ,然后根据等腰三角形的性质,求得FK:FC=1:8,设FK=x,求得AF:AC的值,即可求得S△ABF的值.
,然后根据等腰三角形的性质,求得FK:FC=1:8,设FK=x,求得AF:AC的值,即可求得S△ABF的值.解答:
 解:过点E作EK∥CD交AC于K,
解:过点E作EK∥CD交AC于K,∴
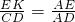 =
=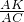 ,
,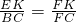 ,
,∵AE:ED=1:3,
∴AE:AD=1:4,
∴
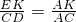 =
= ,
,∵AB=AC,AD⊥BC,
∴BC=2CD,
∴EK:BC=1:8,
∴FK:FC=1:8,
设FK=x,则CK=7x,
∴AK=
 x,
x,∴AC=AK+CK=
 x,
x,∴AF=AK-FK=
 x-x=
x-x= x,
x,∴AF:AC=1:7,
∵S△ABC=21,
∴S△ABF=
 S△ABC=3.
S△ABC=3.故答案为:3.
点评:此题考查了平行线分线段成比例定理、等腰三角形的性质以及等高三角形面积的关系.此题难度较大,解题的关键是准确作出辅助线,利用数形结合思想与方程思想求解.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
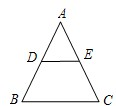 如图,已知等腰△ABC的面积为8cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面积为
如图,已知等腰△ABC的面积为8cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面积为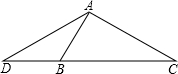 如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB.
如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB. (2010•西藏)如图,已知等腰△ABC,AC=BC=10,AB=12,以BC为直径作⊙O交AB点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(2010•西藏)如图,已知等腰△ABC,AC=BC=10,AB=12,以BC为直径作⊙O交AB点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E. 如图,已知等腰△ABC中,AB=AC,P、Q分别为AC、AB上的点,且AP=PQ=QB=BC,则∠PCQ的度数为( )
如图,已知等腰△ABC中,AB=AC,P、Q分别为AC、AB上的点,且AP=PQ=QB=BC,则∠PCQ的度数为( ) 如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,
如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,