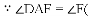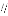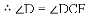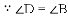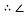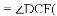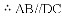题目内容
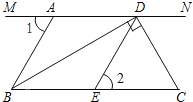
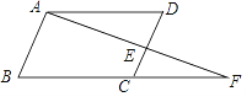
如图1,四边形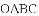
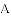
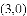
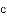
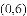
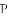
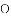
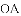
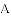
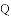
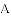
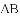
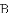

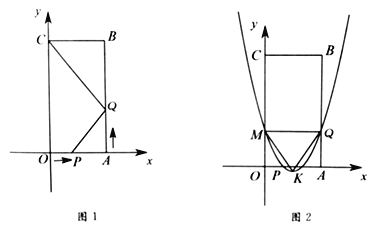
(1)当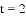
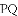
(2)当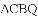
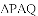

(3)当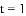
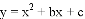 经过
经过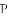
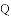
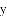
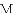
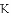
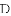
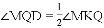 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的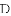
练习册系列答案
相关题目


 ,求AC的长.
,求AC的长.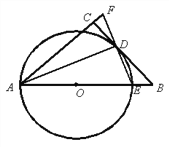
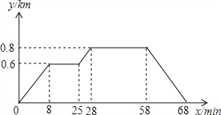
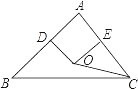
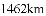
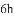
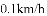
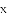
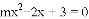 有两个不相等的实数根,那么
有两个不相等的实数根,那么