题目内容
已知二次函数y=x2-2mx-2m2(m≠0)的图象与x轴交于A、B两点,它的顶点在以AB为直径的圆上.
(1)证明:A、B是x轴上两个不同的交点;
(2)求二次函数的解析式;
(3)设以AB为直径的圆与y轴交于C,D,求弦CD的长.
(1)证明:∵y=x2-2mx-2m2(m≠0),
∴a=1,b=-2m,c=-2m2,
△=b2-4ac=(-2m)2-4×1×(-2m2)=4m2+8m2=12m2,
∵m≠0,
∴△=12m2>0,
∴A,B是x轴上两个不同的交点;
(2)设AB点的坐标分别为A(x1,0),B(x2,0),
则x1+x2=- =2m,x1•x2=
=2m,x1•x2= =-2m2,
=-2m2,
∴AB=|x1-x2|=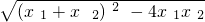 =2
=2 |m|,
|m|,
∵抛物线的顶点坐标为:(m,-3m2),且在以AB为直径的圆上,
∴AB=2×3m2,
∴2 |m|=6m2,
|m|=6m2,
∴m=± ,
,
∴y=x2± x-
x- ;
;
(3)根据(2)的结论,圆的半径为 ×6m2=
×6m2= ×2=1,
×2=1,
弦CD的弦心距为|m|= ,
,
∴ CD=
CD=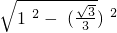 =
= ,
,
∴CD= .
.
分析:(1)求出根的判别式,然后根据根的判别式大于0即可判断与x轴有两个交点;
(2)利用根与系数的关系求出AB的长度,也就是圆的直径,根据顶点公式求出顶点的坐标得到圆的半径,然后根据直径是半径的2倍列式即可求出m的值,再把m的值代入二次函数解析式便不难求出函数解析式;
(3)根据(2)中的结论,求出圆的半径,弦心距,半弦,然后利用勾股定理列式求出半弦长,弦CD的长等于半弦的2倍.
点评:本题综合考查了二次函数与x轴的交点的个数的判断,根与系数关系的应用,以及圆的半径,弦心距,半弦长构成直角三角形的应用,勾股定理,综合性较强,但难度不是很大仔细分析求解便不难解决.
∴a=1,b=-2m,c=-2m2,
△=b2-4ac=(-2m)2-4×1×(-2m2)=4m2+8m2=12m2,
∵m≠0,
∴△=12m2>0,
∴A,B是x轴上两个不同的交点;
(2)设AB点的坐标分别为A(x1,0),B(x2,0),
则x1+x2=-
 =2m,x1•x2=
=2m,x1•x2= =-2m2,
=-2m2,∴AB=|x1-x2|=
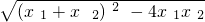 =2
=2 |m|,
|m|,∵抛物线的顶点坐标为:(m,-3m2),且在以AB为直径的圆上,
∴AB=2×3m2,
∴2
 |m|=6m2,
|m|=6m2,∴m=±
 ,
,∴y=x2±
 x-
x- ;
;(3)根据(2)的结论,圆的半径为
 ×6m2=
×6m2= ×2=1,
×2=1,弦CD的弦心距为|m|=
 ,
,∴
 CD=
CD=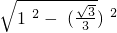 =
= ,
,∴CD=
 .
.分析:(1)求出根的判别式,然后根据根的判别式大于0即可判断与x轴有两个交点;
(2)利用根与系数的关系求出AB的长度,也就是圆的直径,根据顶点公式求出顶点的坐标得到圆的半径,然后根据直径是半径的2倍列式即可求出m的值,再把m的值代入二次函数解析式便不难求出函数解析式;
(3)根据(2)中的结论,求出圆的半径,弦心距,半弦,然后利用勾股定理列式求出半弦长,弦CD的长等于半弦的2倍.
点评:本题综合考查了二次函数与x轴的交点的个数的判断,根与系数关系的应用,以及圆的半径,弦心距,半弦长构成直角三角形的应用,勾股定理,综合性较强,但难度不是很大仔细分析求解便不难解决.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
已知二次函数y=x2+(2a+1)x+a2-1的最小值为0,则a的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).