题目内容

如果x-y= $数学公式$ +1，y-z= $数学公式$ -1，那么x²+y²+z²-xy-yz-zx=________．

7
分析：根据已知的两个等式，相加可得x-z=2 $\text{[math]}$ ③，再求①²+②²+③²的值，整理化简即可求x²+y²+z²-xy-yz-yx的值．
解答：∵x-y= $\text{[math]}$ +1①，y-z= $\text{[math]}$ -1②，
∴x-z=2 $\text{[math]}$ ③，
则①²+②²+③²=（x-y）²+（y-z）²+（x-z）²=（ $\text{[math]}$ +1）²+（ $\text{[math]}$ -1）²+（2 $\text{[math]}$ ）²=14，
即2（x²+y²+z²-xy-yz-yx）=14，
∴x²+y²+z²-xy-yz-yx=7．
故答案为：7．
点评：本题主要考查完全平方公式．完全平方公式：（a±b）²=a²±2ab+b²．

练习册系列答案

Happy holiday快乐假期暑假作业延边教育出版社系列答案

假期总动员四川师范大学电子出版社系列答案

暑假训练营学年总复习希望出版社系列答案

滴水穿石初中暑假快乐提升晨光出版社系列答案

暑假作业本浙江教育出版社系列答案

学习与探究暑假学习系列答案

名校假期作业西安出版社系列答案

新路学业快乐假期暑假作业新疆青少年出版社系列答案

暑假作业及活动新疆美术摄影出版社系列答案

快乐暑假假日乐园广西师范大学出版社系列答案

相关题目

如果关于x的不等式组

2x-10(m-1)＞5m-5x

无解，则m的取值范围是（　　）

A、m＞3	B、m≥3
C、m＜3	D、m≤3

5、下列说法中正确的个数有（　　）
①对角线互相平分且相等的四边形是菱形；
②有一组对边平行的四边形是梯形；
③如果四边形的两条对角线互相垂直，那么它的面积等于两条对角线长的积的一半；
④如果一个四边形绕对角线的交点旋转90°后，所得图形与原来的图形重合，那么这个四边形是正方形．

如图，正方形ABCD的对角线AC和BD相交于点O，O又是正方形A₁B₁C₁O的一个顶点，O A₁交AB

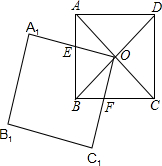于点E，OC₁交BC于点F．
（1）求证：△AOE≌△BOF；
（2）如果两个正方形的边长都为a，那么正方形A₁B₁C₁O绕O点转动，两个正方形重叠部分的面积等于多少？为什么？

2010年2月中旬，沿海各地再次出现用工荒，甲乙两人是技术熟练的工人，他们参加一次招聘会，听说有三家企业需要他们这类人才，虽然对三家企业的待遇状况不了解，但是他们一定会在这三家企业中的一家工作．三家企业在招聘中有相同的规定：技术熟练的工人只要愿意来，一定招，但是不招在招聘会中放弃过本企业的工人．甲乙两人采用了不同的求职方案：
甲无论如何选位置靠前的第一家企业；而乙则喜欢先观察比较后选择，位置靠前的第一家企业，他总是仔细了解企业的待遇和状况后，选择放弃；如果第二家企业的待遇状况比第一家好，他就选择第二家企业；如果第二家企业不比第一家好，他就只能选择第三家企业．
如果把这三家企业的待遇状况分为好、中、差三个等级，请尝试解决下列问题：
（1）好、中、差三家企业按出现的先后顺序共有几种不同的可能？
（2）你认为甲、乙两人采用的方案，哪一种方案使自己找到待遇状况好的企业的可能性大？请说明理由？

某学校七年级数学兴趣小组组织一次数学活动．在一座有三道环形路的数字迷宫的每个进口处都标记着一个数，要求进入者把自己当做数“1”，进入时必须乘进口处的数，并将结果带到下一个进口，依次累乘下去，在通过最后一个进口时，只有乘积是5的倍数，才可以进入迷宫中心，现让一名5岁小朋友小军从最外环任一个进口进入．
（1）小军能进入迷宫中心的概率是多少？请画出树状图进行说明；
（2）小组两位组员小张和小李商量做一个小游戏，以猜测小军进迷宫的结果比胜负．游戏规则规完：小军如果能进入迷宫中心，小张和小李各得1分；小军如果不能进入迷宫中心，则他在最后一个进口处所得乘积是奇数时，小张得3分，所得乘积是偶数时，小李得3分，你认为这个游戏公平吗？如果公平，请说明理由；如果不公平，请在第二道环进口处的两个数中改变其中一个数使游戏公平．
（3）在（2）的游戏规则下，让小军从最外环进口任意进入10次，最终小张和小李的总得分之和不超过28分

，请问小军至少几次进入迷宫中心？