题目内容

7．如图，在△ABC中，∠C=90°，BD是∠ABC的平分线，若AC=12，AD=8，求点D到AB的距离．

分析 过点D作DE⊥AB于E，然后求出CD的长，再根据角平分线上的点到角的两边的距离相等可得DE=CD．

解答 解：如图，过点D作DE⊥AB于E，
∵CA=12，AD=8，
∴CD=CA-AD=12-8=4，
∵BD是∠ABC的平分线，
∴DE=CD=4，
故D到AB的距离是4．

点评 本题考查了角平分线上的点到角的两边的距离相等的性质，熟记性质是解题的关键．

练习册系列答案
相关题目
17．如果$\sqrt{{a}^{2}}$=-a，那么a的取值范围是（　　）
A．正数B．负数C．非负数D．非正数
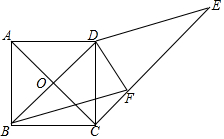18．如图，正方形ABCD的边长为1，对角线交于点O，作∠DBF=30°，CE∥BD，DE∥BF，CE与BF交于点F，连接DF，∠DFC=105°．
（1）求证：四边形BDEF是菱形；
（2）试说明△BDF的面积等于△ABD的面积；
（3）求CF的长．
15．已知x，y是实数，且y=$\frac{{\sqrt{{x^2}-9}+\sqrt{9-{x^2}}-2}}{x+3}$，求5x+6y的值．
2．下列计算正确的是（　　）
A．2a-a=2B．x3+x3=x6C．a2•b2=（ab）4D．2t2+t2=3t2
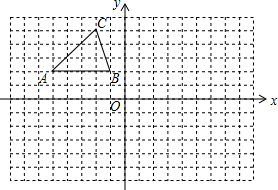12．把△ABC向下平移8个单位后得到对应的△A1B1C1，画出△A1B1C1（要求尺规作图，并且保留作图痕迹）
19．下列图形中，是中心对称图形的是（　　）
A．B．C．D．
16．如果x2+kx+9是一个完全平方式，那么k的值是±6．
17．如图，将△ABC沿射线BC方向平移3cm得到△DEF．若△ABC的周长为14cm，则四边形ABFD的周长为（　　）
A．14 cmB．17 cmC．20 cmD．23 cm

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网